乗算は乗数の各桁に対応する部分積を作り、それら全ての合計を求めるというのがパラレルアダーの基本的な考え方であるが、乗数の最下位の桁に対応する部分積から順に加算を行う必要は無い。例えば、1234 x 368を計算する場合、
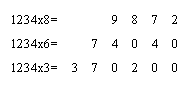 |
と3つの部分積があるが、筆算を行う場合は、最初の2つの部分積の和を計算し終わってから、その合計に3つ目の部分積を足すということはやらない。桁を合わせて全部の部分積を書いて、まず、全部の部分積の1の桁の合計を求め、次にその桁上がりを含めて部分積の10の桁の合計を求め、次にその桁上がりを含めて部分積の100の桁の合計を求めるというように計算を行う。こうすれば、部分積の加算1回ごとにキャリーを伝搬させる必要がなく、計算が簡単となる。これを図示すると次のようになる。
 |
|
筆算の計算順序 |
この考え方を2進数の世界で実現するのが、Wallace氏が考案したWallace Tree(ウォレス ツリー)である。Radix-4のブースエンコーダを使って部分積を作ると、2ビットずれた部分積が作られ、全体としては次の図のように、斜めになった平行四辺形の形に部分積のビットが並ぶことになる。
 |
各桁の部分積の合計を求めるのであるが、枠で囲まれた中央付近の桁では部分積の個数分のビットが入力となるが、平行四辺形であるので、下位と上位のビットでは入力数は減少する。部分積の合計であるが、各桁の要素は2進数1ビットであるので、合計を求めるということはその桁にある"1"の個数を数えることになる。そのため、この計算を行うエレメントはカウンタとも呼ばれる。
次の図で、三角形で示したカウンタは、入力に"1"が2個以上あれば、左の辺から出ている桁上り信号を"1"とし、入力の"1"の個数が1個か3個の場合に出力が"1"になるという回路であり、これは実は1ビットのフルアダーである。そして、このカウンタを使った、一桁分のWallace Treeは次の図のようになる。
 |
|
各桁のWallace Treeの構成。12個の部分積の加算の例 |
この図は12個の部分積を加算する構成で、12個の部分積が上側から入ってきて、そして、下位の桁の桁上り信号が第2段に4つ、第3段に3つ、第4段と第5段に合計3つ入力できる。そして、上位の桁に対する桁上り信号が、第1段から4つ、第2段から3つ、第3段と第4段から3つ出ている。
従って、第1段からの桁上り信号を上位の桁の第2段の入力、第2段の桁上り出力を上位の桁の第3段の入力という風に接続して行けば、部分積入力から各桁のサムとキャリーまでのカウンタの通過段数は積のビット数が大きくなっても増加せず、部分積の数で決まる一定の段数のカウンタのツリーで各桁の"1"の個数を求めることができる。これがウォレスツリーのメリットである。
なお、部分積の図に見られるように、入力数は下位と上位の桁では少なくなり、これらの桁では入力数が少なくなるので不要となるカウンタは削除して良い。そして、上記のツリーでは、各桁の出力はサムと上位の桁へのキャリー信号となっており、最終的な積を求めるためには、このサムとキャリーをキャリー伝搬型のアダーを用いて加算する必要がある。このアダーとしては、当コラムで説明したKogge-Stoneアダーなどを用いれば良い。
ということで、Wallace Tree方式の部分積の合計を求める回路は、全体では次の図のようになる。この図においてWiで示したボックスは、前に構造を示した1桁分のウォレスツリーである。
 |
|
部分積を加算するWallace Tree。Wiの箱が1桁の加算回路で、部分積のビットと下位のWjの箱からの桁上り分を加算する。 |
このBooth EncoderとWallace Treeはどちらも巧妙な回路であり、現代の高性能マイクロプロセサの乗算器は、殆どがこの方式で作らていると言っても過言ではない。