見やすい「3-D 縦棒」のグラフを作る（前編）

Excelには「3-D 縦棒」と呼ばれる立体グラフを作成する機能も用意されている。ただし、立体化したグラフは数値を読み取りにくくなるため、実際に使用されているケースはあまり多くないようだ。そこで今回は「3-D 縦棒」のグラフを少しでも見やすくするためのカスタマイズ方法を紹介していこう。

自動作成される「3-D 縦棒」のグラフ

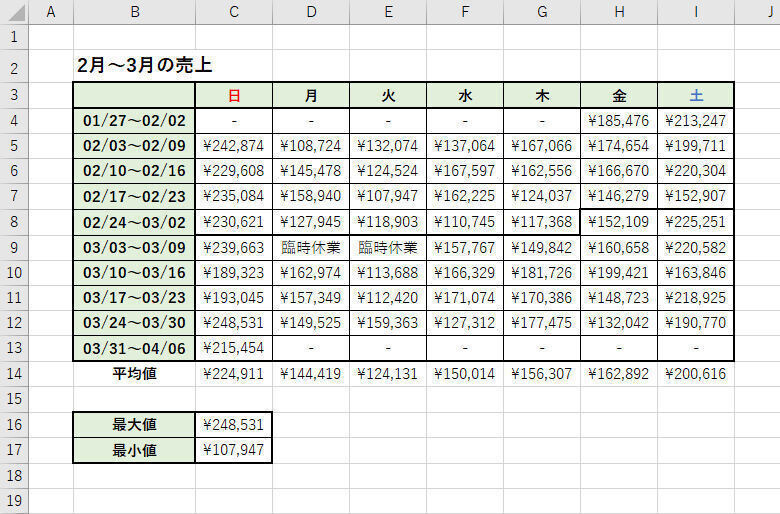
今回は、以下の図に示したデータを使ってグラフのカスタマイズ手順を紹介していく。このデータは、ある企業が新たに開始したサービスについて「どれくらい一般に知られているか？」を年代別に調査したものだ。直近の1年間について毎月、認知度を調査した結果となる。

このデータをもとに普通に「集合縦棒」のグラフを作成すると、以下の図のような結果が得られる。

• 

  「集合縦棒」でグラフを示した場合

大まかな傾向は把握できるものの、年代別のデータ推移を一目で理解できるグラフにはなっていない。そこで、今度は「3-D 縦棒」のグラフを作成してみよう。「3-D 縦棒」のグラフを作成するときは「挿入」タブを選択し、以下の図のように操作すればよい。

• 

  「3-D 縦棒」の作成手順

すると、棒グラフを年代別に並べた立体グラフを作成できる。とはいえ、こちらも「見やすいグラフ」とは言い難いのが実情だ。

• 

  自動作成された「3-D 縦棒」のグラフ

このグラフをカスタマイズしていき、以下の図のようなグラフに仕上げていくのが今回の趣旨となる。

• 

  カスタマイズした「3-D 縦棒」のグラフ

なお、こういったデータをグラフ化するときは「折れ線グラフ」を使用するのが一般的な正解といえるが、今回はあえて「3-D 縦棒」でグラフを表現してみよう。

• 

  「マーカー付き折れ線」でグラフを示した場合

軸の設定変更

それでは、具体的なカスタマイズ手順を紹介していこう。現状では数値データの大きい系列が前面に配置されているため、その背面に並ぶ系列を読み取りにくくなっている。これを改善するには「奥行きの軸」に注目するとよい。「奥行きの軸」を右クリックし、「軸の書式設定」を選択する。

• 

  「軸の書式設定」の呼び出し

すると、以下の図のような設定画面が表示される。ここで「軸を反転する」をONにすると、系列を並べる順番を逆にすることができる。

• 

  「軸を反転する」をONにする

この設定変更だけでも「3-D 縦棒」のグラフが見やすくなるのを感じられるだろう。このように「3-D 縦棒」のグラフでは、数値データの小さい系列ほど手前に配置するのが基本だ。

• 

  軸を反転した「3-D回転」のグラフ

続いては、グラフの左端に配置されている「縦軸」（0.0％～70.0％の数値）に注目してみよう。これらの数値は右端に配置した方がグラフを読み取りやすくなる。この際に注意すべき点は、「縦軸」ではなく、「横軸」の書式設定を変更すること。「横軸」を右クリックし、「軸の書式設定」を選択する。

• 

  「軸の書式設定」の呼び出し

「軸の書式設定」が表示されるので、「縦軸との交点」を「最大項目」に変更する。すると、0.0％～70.0％の数値をグラフの右端に配置できる。

• 

  「縦軸との交点」を「最大項目」に変更

• 

  「縦軸」を右端に配置したグラフ

X方向、Y方向の回転角度

続いては、「3-D 縦棒」ならではの設定項目といえる「奥行き」と「回転角度」について紹介していこう。これらの設定画面は「プロットエリア」を右クリックし、「3-D 回転」を選択すると表示できる。

• 

  「3-D 回転」の書式設定の呼び出し

まずは「奥行き」の設定項目を調整する。この数値を大きくすればするほど、奥行き方向のサイズが大きくなる。

• 

  「奥行き」の調整

たとえば、「奥行き」を350（％）に変更すると、奥行き方向のサイズを3.5倍にしたグラフにカスタマイズできる。各系列の間隔が広くなるぶんだけ「グラフが見やすくなる」といえるだろう。

• 

  「奥行き」を350に変更したグラフ

また、グラフを見る視点の位置を調整することも可能だ。この場合は、「X方向に回転」と「Y方向に回転」の数値を調整する。

たとえば「X方向に回転」の数値を大きくすると、より右側に回り込んでグラフを見たような形にカスタマイズできる。

• 

  「X方向に回転」を30度に変更した例

一方、「Y方向に回転」の数値を大きくすると、より上から覗き込んだような形にグラフをカスタマイズできる。

• 

  「Y方向に回転」を30度に変更した例

これら2つの数値を調整することで、最も見やすい角度を見つけ出すとよい。今回の例では、X方向に5度、Y方向に15度だけ回転した位置に視点を設定してみた。

• 

  X方向に5度、Y方向に15度回転させたグラフ

グラフ内に表示する要素の調整

続いては、グラフ内に表示する要素を調整していこう。

「奥行き」のサイズを十分に確保できている場合は、「奥行きの軸」にそれぞれの項目名が表示されているはずだ。よって、「凡例」を必ずしも表示しておく必要はない。「凡例」を消去すると、そのぶんグラフを広く描画できるので、可能であれば消去しておくとよい。

また、縦方向の目盛線を表示しておくと、各項目の対応を把握しやすくなる。こちらは「目盛線」→「第1主縦軸」をONにすると表示できる。

• 

  「凡例」の消去と「縦軸の目盛線」の表示

さらに、「グラフ タイトル」の配置にも注意しておく必要がある。「3-D 回転」のグラフは上下の余白が大きすぎる傾向があるため、「グラフ タイトル」を重ねて配置しても十分な余白を確保できる。「グラフ タイトル」→「グラフを中央揃えで重ねて配置」を選択し、配置方法を変更しておこう。

• 

  「グラフ タイトル」の配置変更

これらの設定変更を施すと、上下方向の無駄な余白がなくなり、領域全体にグラフを大きく描画できるようになる。

• 

  「グラフ タイトル」の配置を変更したグラフ

このように「3-D 縦棒」のグラフは、書式の設定次第でグラフの見た目を大幅に改善することが可能である。

今回の連載で紹介した書式のほかにも「色の変更」や「間隔の調整」など、「3-D 縦棒」の見た目を改善できる箇所はまだまだある。これらも紹介していくと少し話が長くなってしまうので、この続きについては次回の連載で詳しく紹介していこう。