前回の連載では、RANDやRANDBETWEEN、RANDARRAYなどを使って「数値データ」をランダムに生成する方法を紹介した。今回はその応用編ということで、関数RANDを使って「文字列データ」をランダムに生成する方法を紹介していこう。手順そのものは特に難しくないが、「生成されるデータの割合をどうコントロールするか？」に配慮する必要がある。

文字列データをランダムに生成するには？

今回も「Excelの使い方を学習するためのダミーのデータ表」を作成する方法を紹介していこう。前回の連載の続編となる話なので、第61回の連載を一読してから本連載を読み進めて頂ければ幸いだ。

乱数（ランダムな数値データ）をもとに「文字列データ」を生成するときは、IFやIFSといった関数を組み合わせて使用するとよい。

  • RANDとIF、IFSを組み合わせたダミーデータの作成

今回も「前回と同じデータ表」を使って手順を紹介していこう。前回の連載では、「年齢」の数値データをRANDやRANDBETWEEN、RANDARRAYといった関数で作成する方法を紹介した。これを応用してダミーの「性別」や「都道府県」のデータをランダムに自動作成してみよう。

  • Excelの練習用に作成するダミーの名簿

2種類の文字列データをランダムに生成する

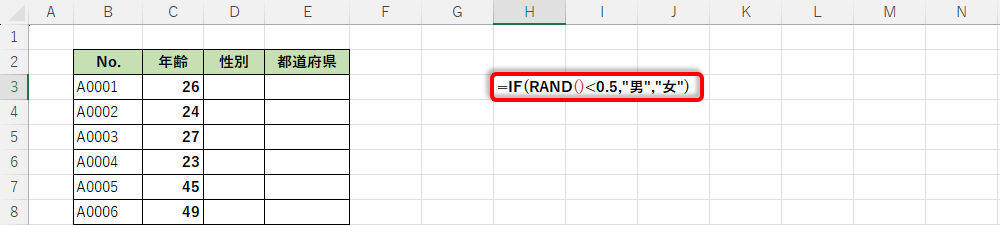
まずは「性別」のデータをランダムに生成する方法から紹介していこう。この列に記載すべきデータは「男」または「女」の2種類だ。このように「2種類の文字列データ」を生成したいときは、IFとRANDを組み合わせて以下のように関数を記述すればよい。

  • 関数IFと関数RANDを組み合わせて入力

  • 関数の結果

簡単に説明しておこう。関数が入れ子に記述されているときは、内側の記述から処理内容を確認していくのが基本だ。上図に示した例の場合、以下の手順で処理が進められていくことになる。

（1）関数RANDにより「0～1未満」の数値（乱数）が生成される
（2）この数値が「0.5未満であるか？」を条件に分岐処理を行う
　　・0.5未満の場合 ・・・・「男」の文字列データを出力
　　・そうでない場合 ・・・・「女」の文字列データを出力

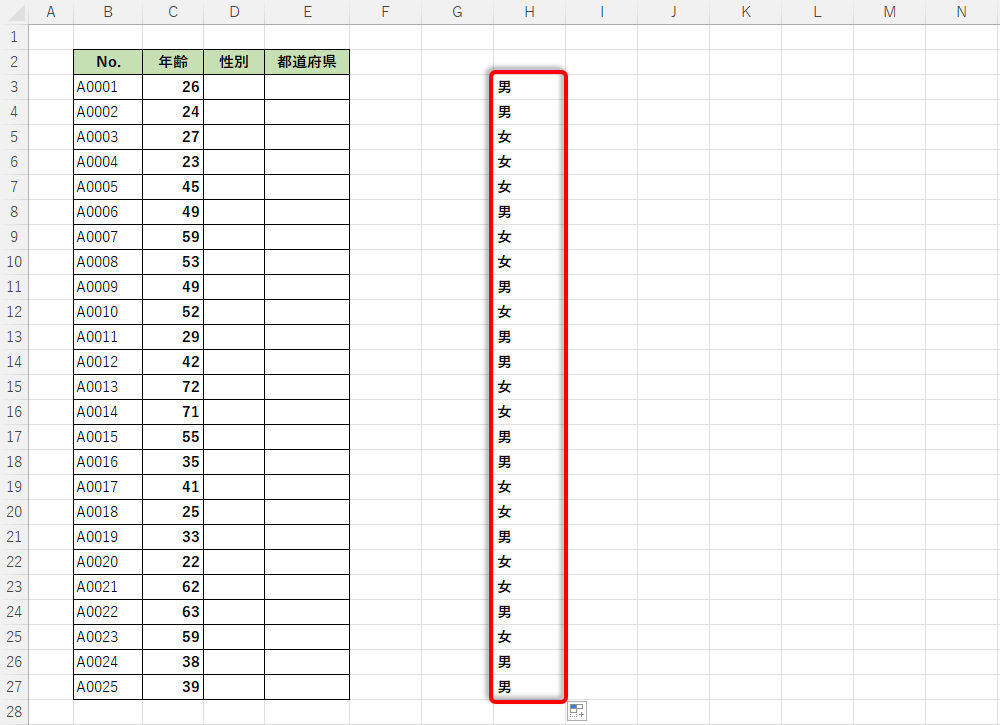
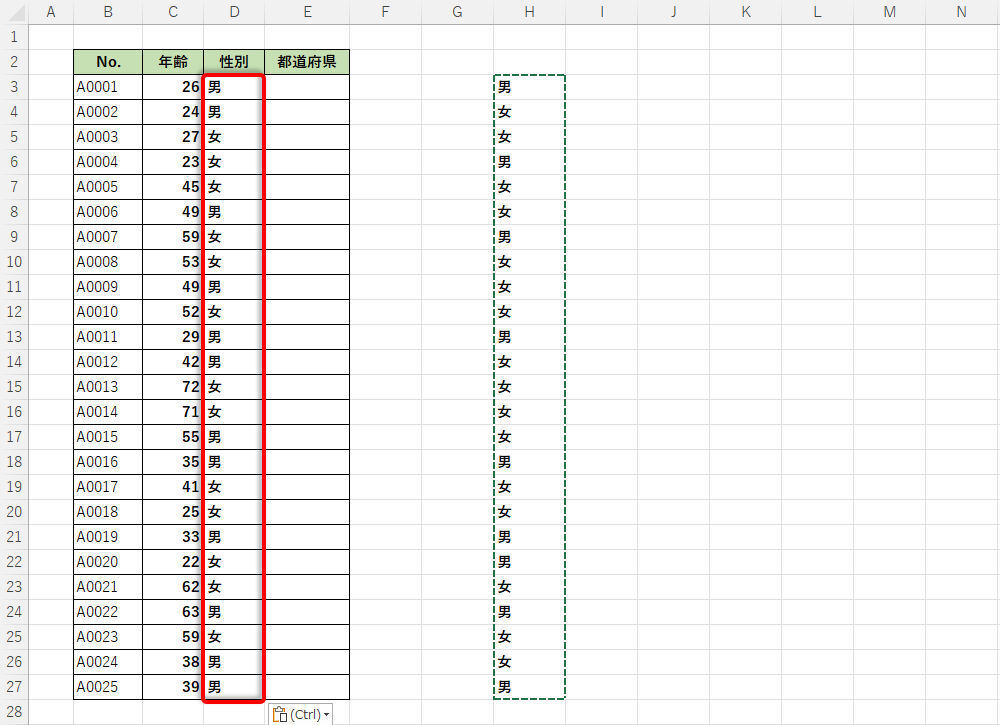
このように処理を進めていくことで「男」または「女」の文字列データをランダムに生成している。あとは、この関数をオートフィルでコピーするだけ。これで好きな数だけ「男」または「女」の文字列データをランダムに生成することが可能となる。

  • 関数をオートフィルでコピーした様子

特に難しい処理は行っていないので、RANDとIFの使い方さえ知っていれば内容を理解できるだろう。

なお、前回の連載でも紹介したように、関数RANDは「何らかの操作を行うたびに乱数を再生成する」という点にも注意しなければならない。生成した「男」または「女」のデータを固定したいときは、コピー＆ペーストで「値」だけを貼り付ける操作を行っておく必要がある（詳しくは第61回の連載を参照）。

  • 生成した「男・女」のデータを「値」として貼り付け

これで男：女の比率が1：1のデータをランダムに作成できた。もちろん、それぞれの比率を調整することも可能だ。たとえば、男性6割、女性4割の比率でデータを作成したいときは、「=IF(RAND()<0.6,"男","女")」のように関数を記述すればよい。

3種類以上の文字列データをランダムに生成する

続いては、「3種類以上の文字列データ」をランダムに生成する方法として「都道府県」のダミーデータを作成してみよう。この場合は、関数IFSなどを使って処理を3つ以上に分岐してあげればよい。

ここでは、「東京都」、「神奈川県」、「埼玉県」、「千葉県」といった4種類の文字列データをランダムに生成する場合を例に手順を紹介していこう。

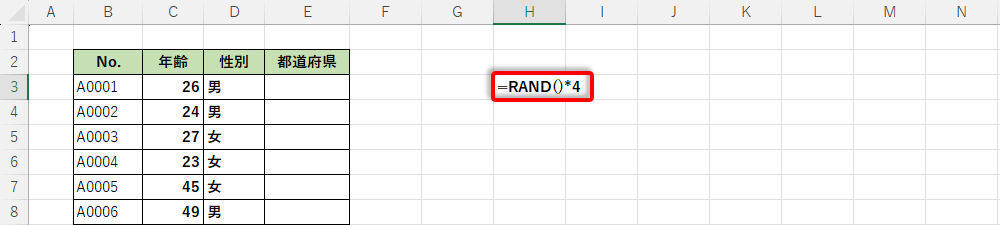
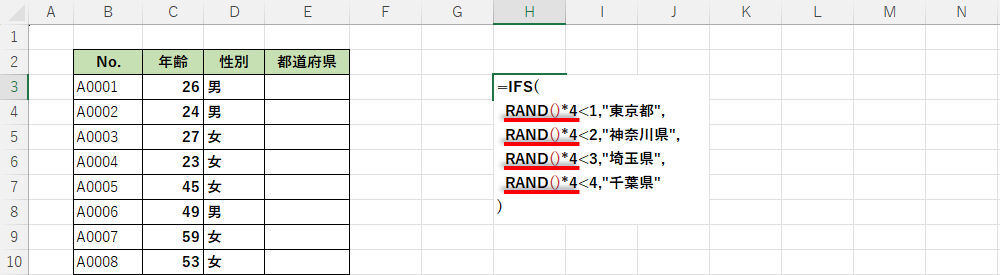
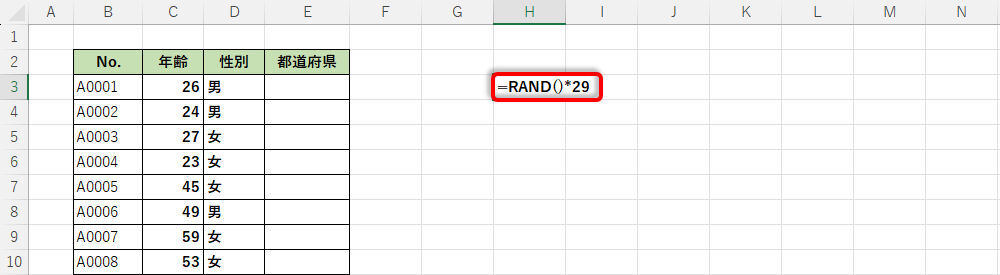
最初に紹介するのは最も単純でシンプルな考え方だ。まずは、関数RANDを4倍して「0～4未満」の数値（乱数）を生成する。

  • 関数RANDで0～4未満の数値データを生成

続いて、この数値（H3セル）に応じて出力する文字列データを変化させる。具体的には、

・1未満の場合は「東京都」を出力
・2未満の場合は「神奈川県」を出力（1以上、2未満）
・3未満の場合は「埼玉県」を出力（2以上、3未満）
・4未満の場合は「千葉県」を出力（3以上、4未満）

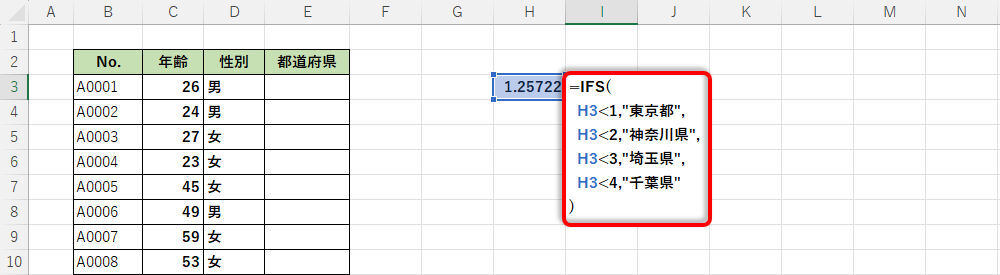
という分岐処理を関数IFSで実現すればよい。処理内容を把握しやすいように、「Alt」＋「Enter」で改行した記述例を紹介しておこう。

  • 数値に応じて「文字列データ」を変化させる関数IFS

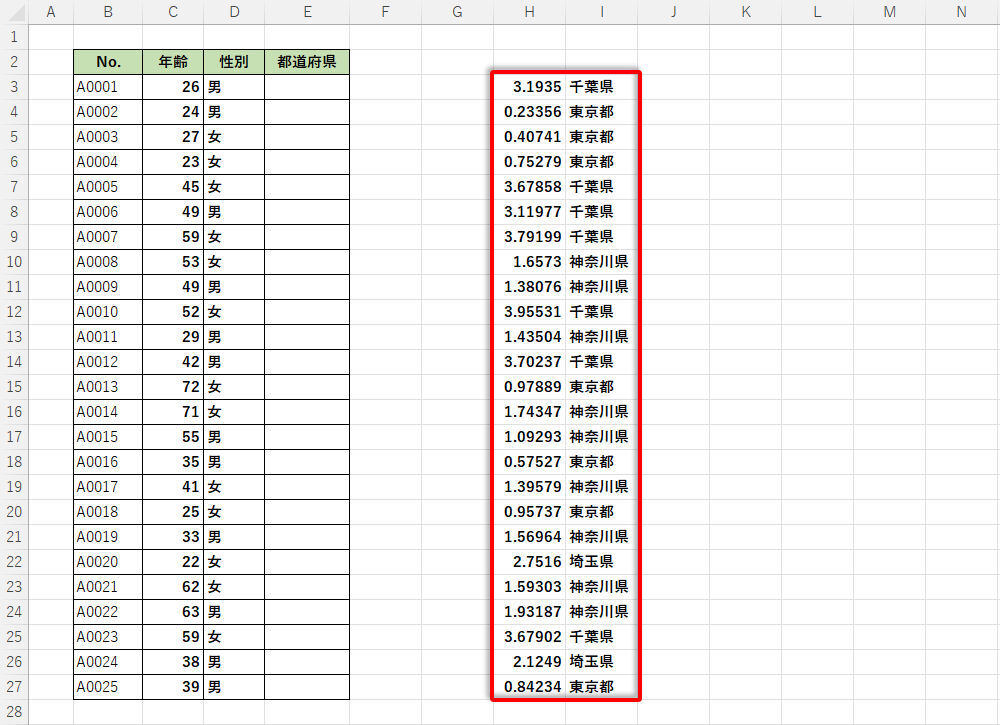
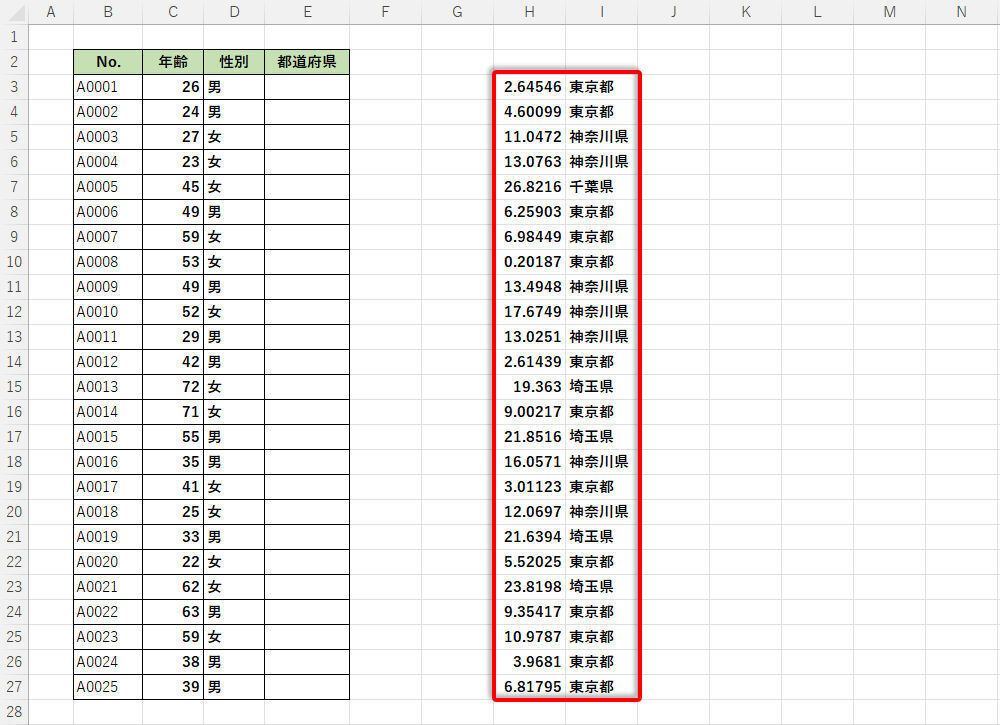
あとは、これらの関数をオートフィルでコピーするだけ。これで好きな数だけ「東京都」、「神奈川県」、「埼玉県」、「千葉県」の文字列データをランダムに生成できる。

  • 関数をオートフィルでコピーした様子

参考までに「各データの生成割合」も紹介しておこう。以下の図は、上記に示した方法で「都道府県」のデータを100個ずつ生成する処理を8回試行した実験結果となる。

  • 各データが生成される割合

乱数を使用しているため、試行ごとに“ばらつき”はあるものの、おおよそ1/4（25個）の確率で各データが出力されているのを確認できるだろう。各データを同じ確率で生成したいときは、ここで紹介した手法を用いるのが最も簡単といえる。

IFSとRANDを組み合わせるときの注意点

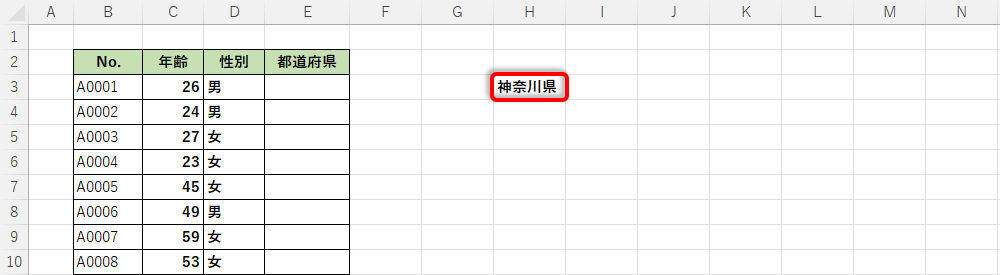
先ほどの例を見たときに、「わざわざ別のセルで乱数を生成するのではなく、IFSの中に組み込んでしまえばよいのに・・・」と感じた方もいるだろう。この場合は、以下の図のように関数を記述することになる。

  • IFSの中に関数RANDを組み込んだ記述

「Enter」キーを押して関数を実行すると、今回の例では「神奈川県」という結果が表示された。

  • 関数IFSの結果

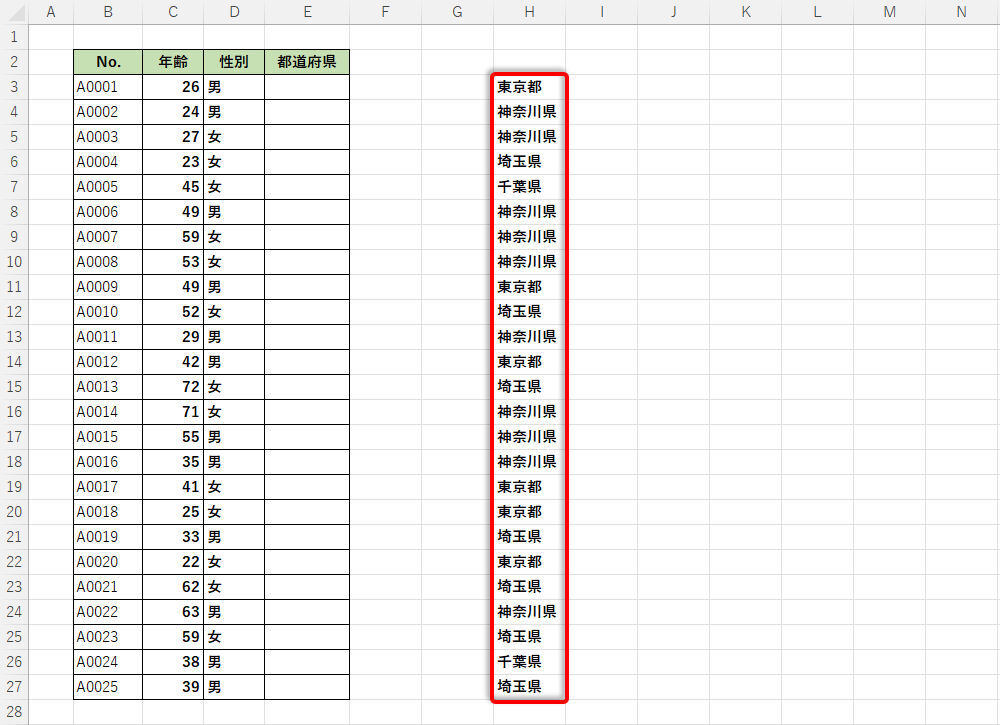
続いて、この関数をオートフィルでコピーすると、以下の図のような結果を得ることができる。

  • 関数IFSをオートフィルでコピーした様子

この方法でも問題なく「4種類の文字列データ」をランダムに生成できると思うかもしれない。しかし、この場合は少しだけ注意が必要となる。

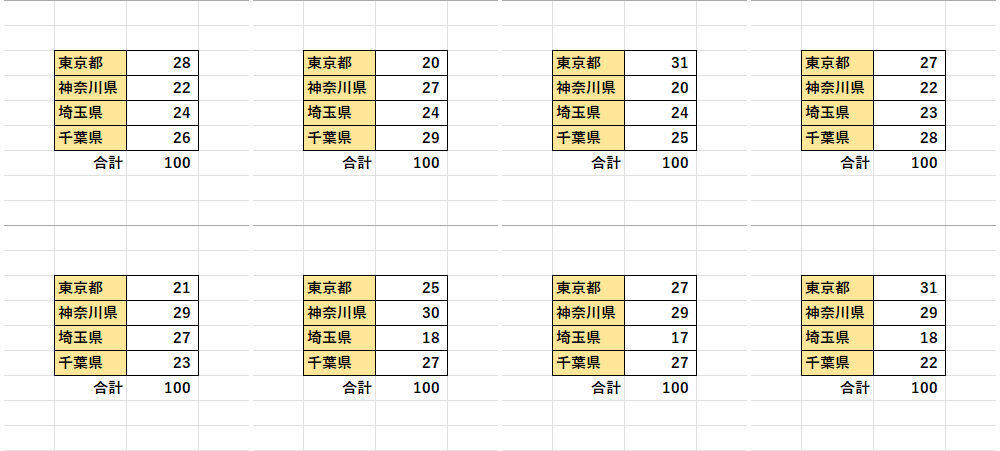
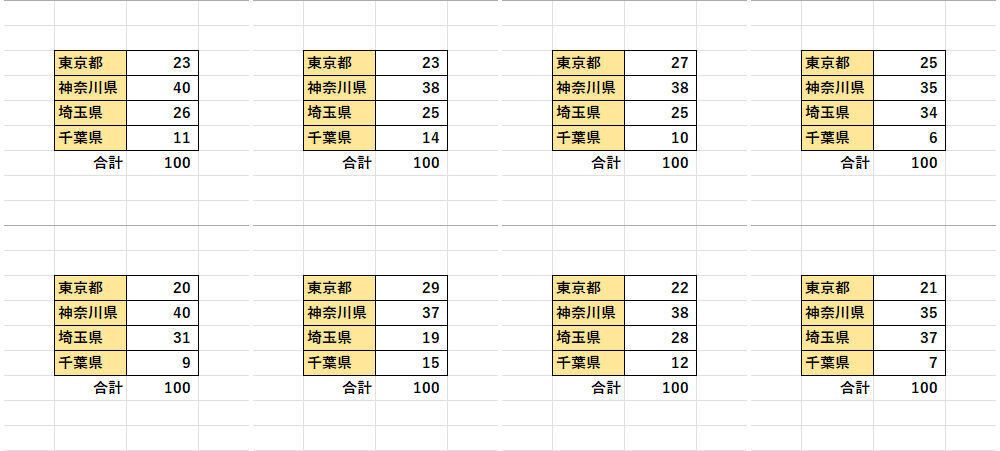
先の例と同様に「各データの生成割合」を確認する実験を行ってみよう。以下の図は、「都道府県」のデータを100個ずつ生成する処理を8回試行したときの実験結果となる。

  • 各データが生成される割合

この結果を見ると、「神奈川県」のデータが生成される割合が高く、「千葉県」のデータは少ない、ということに気付くと思う。乱数による“ばらつき”を考慮しても「差がありすぎる・・・」と感じるのではないだろうか？

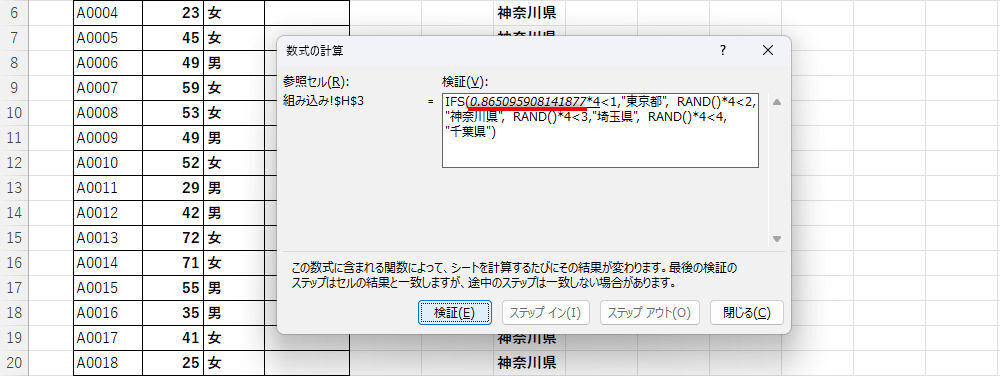
それもそのはず。IFSの中にRANDを組み込む手法には、無視できない問題が潜んでいるからだ。関数の処理内容を確認するために「数式の検証」を行った例を紹介しておこう。

関数を実行すると、最初に「1番目の関数RAND」により乱数が生成される。今回の例では「0.8650・・・」という数値が生成された。

  • 数式の検証（1番目のRANDで生成される値）

この数値を4倍したものは「3.460・・・」となり、「1未満」の条件に合致しない。よって、1番目の条件分岐はFALSEになる。

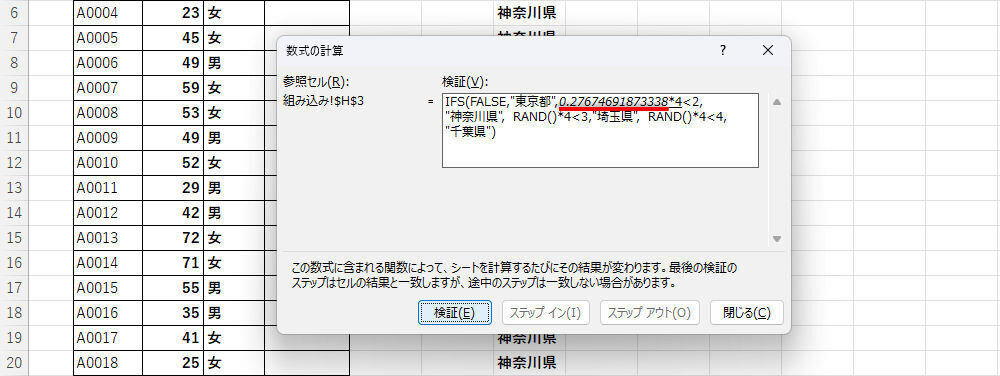
続いて、2番目の条件分岐が処理されていくが、このとき「2番目の関数RAND」により「新しい乱数」が生成されることに注意しなければならない。今回の例では「0.2767・・・」という、先ほどとは異なる数値が生成されている。

  • 数式の検証（2番目のRANDで生成される値）

この数値を4倍したものは「1.1069・・・」となり、「2未満」の条件に合致する。よって、2番目の条件分岐はTRUEになる。

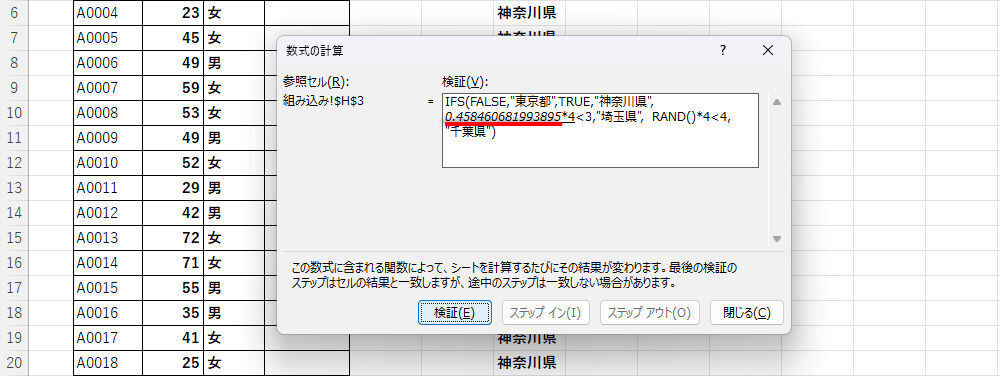
続いて、3番目の条件分岐が処理されていくが、ここでも「3番目の関数RAND」により「新しい乱数」が生成されてしまう。今回の例では「0.4584・・・」という、またまた異なる数値が生成されている。

  • 数式の検証（3番目のRANDで生成される値）

このように、関数IFSの中にRANDを記述した場合は、それぞれの条件分岐処理で「異なる乱数」が生成されることになる。この場合、各データが生成される確率は1/4にならない。それぞれのデータが生成される確率は、

・1番目のデータ ・・・・ 25.000%
・2番目のデータ ・・・・ 37.500%
・3番目のデータ ・・・・ 28.125%
・4番目のデータ ・・・・ 9.375%

となる。関数IFSの中にRANDを組み込むときは、このような問題が潜んでいることに注意しておく必要がある。

比率を変化させながら文字列データを生成するには？

続いては、各データを異なる確率で生成する方法を紹介しておこう。これまでは、東京都／神奈川県／埼玉県／千葉県のデータを“同じ確率”で生成しようとしてきたが、実際の人口分布はそうなっていない。より現実味のあるダミーデータにするために、各データの生成比率を調整したいケースもあるだろう。

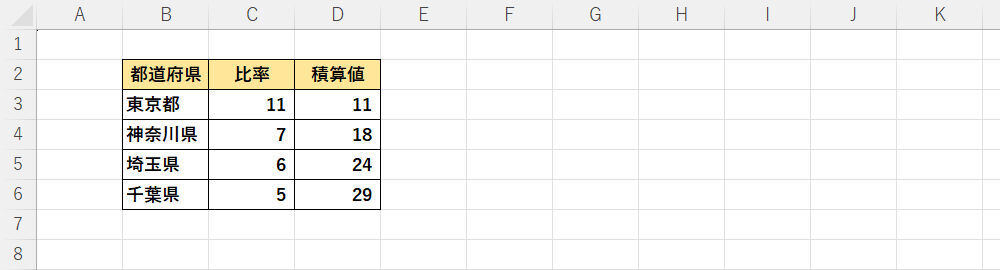
令和2年国勢調査基準によると、日本全体における4都県の人口比率は、東京都が11.24％、神奈川県が7.39％、埼玉県が5.87％、千葉県が5.01％と報告されている（※）。大雑把に見て「11：7：6：5」という比率だ。

（※）https://www.e-stat.go.jp/dbview?sid=0003448233

それぞれの比率を積算（足し算）していくと、以下の図のようになる。

  • 各都道府県の人口比率と積算比率

この比率に従って「文字列データ」をランダムに生成したいときは、以下のように処理を進めていけばよい。まずは、最大値が「最終的な積算値」となるように乱数を生成する。今回の例では「0～29未満」の乱数を関数RANDで生成する。

  • 関数RANDで0～29未満の数値データを生成

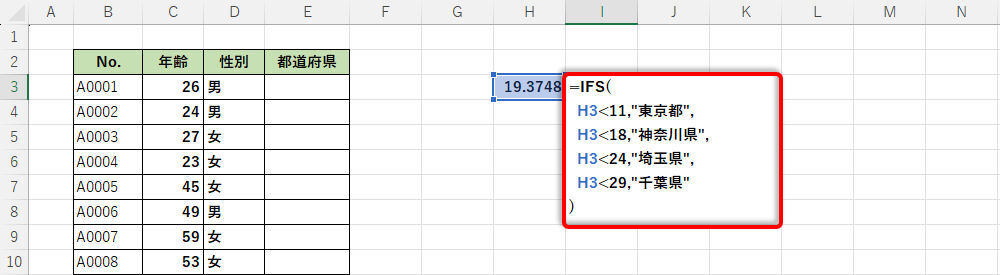
続いて、「各都県の積算値より小さい」を条件に関数IFSで分岐処理を行う。今回の例の場合、以下の図のように条件を記述すればよい。

  • 数値に応じて「文字列データ」を変化させる関数IFS

あとは、この関数をオートフィルでコピーするだけ。これで東京都／神奈川県／埼玉県／千葉県のデータを「11：7：6：5」の比率で生成できるようになる。

  • 関数IFSをオートフィルでコピーした様子

とはいえ、これは理論上の話であり、必ずしも「11：7：6：5」の比率になる訳ではない。乱数を使用しているため、多少の“ばらつき”が生じるのが普通だ。

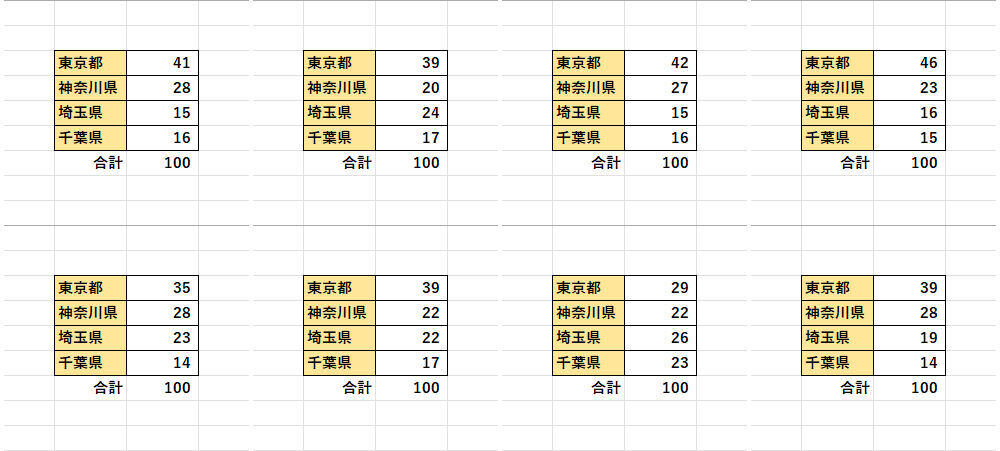
参考までに、これまでと同様に、各データを100個ずつ生成する処理を8回試行したときの実験結果を示しておこう。

  • 各データが生成される割合

この結果を見ると、「東京都」のデータが生成される割合が高く、続いて「神奈川県」、「埼玉県」、「千葉県」という順番でデータが生成されているケースが多い、ということを確認できる。もちろん「必ずしも」ではなく、「全体的に見て、そういう傾向にある」というレベルの話だ。

ダミーデータなので、ここまで厳密にデータを生成する必要はないかもしれないが、データの生成確率を調整する一つの手法として覚えておくと、色々な場面に応用できるかもしれない。