ニューラルネットワークの計算

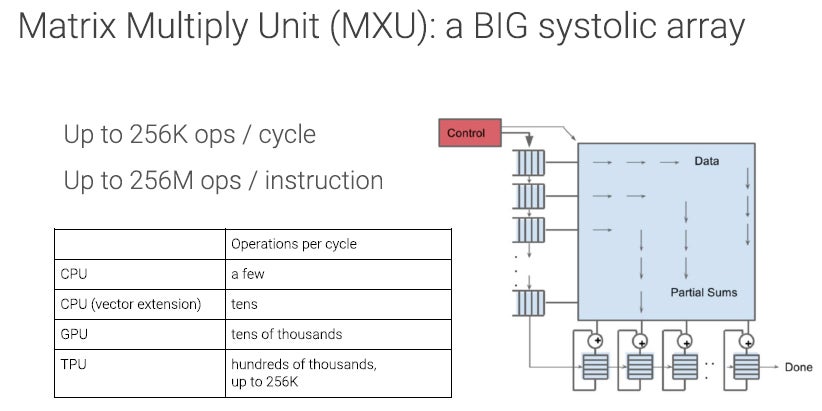
ニューラルネットワークの計算は、入力のマトリクスと重みのマトリクスをかけるという計算が中心である。マトリクスの乗算は、入力Xの行ベクトルと重みWの列ベクトルを掛けることになるが、TPUではシストリックアレイ(Systolic Array)というちょっと特別なやり方で計算を行っている。

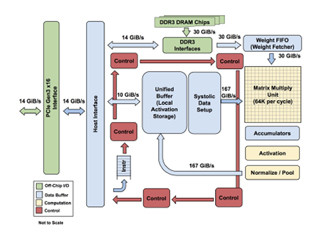
次の図の大きなボックスが256行256列の積和演算器のアレイである。上辺から重みが供給されて積和演算器にプレロードされる。そして左辺から入力Xが供給される。ただし、シストリックアレイでは、256個の入力はユニファイドバッファから同時に読まれるのではなく、1クロックに1個ずつ順番に読まれる。そして256×256の演算器アレイの中で、クロックごとに次の列にシフトされて、その演算器にプレロードされた重みとの積が計算されていく。

このため、最初のサイクルには右上の角の積和演算だけが行われ、次のサイクルには右上の2×2の4個の積和演算、その次は3×3の9積和演算という風に、左上から演算を行う部分が広がっていく。そして、全体に演算が広がると65,536個の積和演算器が全部動作する状態になる。

なお、入力が256より多い場合は1回の計算では足りないので複数回に分割して計算する必要がある。この複数回の部分的な結果を足し込むため、下辺からの出力を足しこむ演算器と4Kエントリのバッファが設けられている。

このマトリクス乗算アレイは64K積和であるので、積と和で2演算と考えると128Kops/cycleであるが、この図では256Kops/cycleと書かれており、積和以外の演算機能があるのかもしれない。しかし、ISCA 44で発表された論文では700MHzクロックで92Topsと書かれており、これは128Kops/cycleに対応する。

  • マトリクス乗算ユニットは1サイクルに最大256K演算を実行

    マトリクス乗算ユニットは1サイクルに最大256K演算を実行。なお、ISCA 44の論文では700MHzクロックで92Tops/s(128K演算/cycle)となっている

TPU v1の性能比較

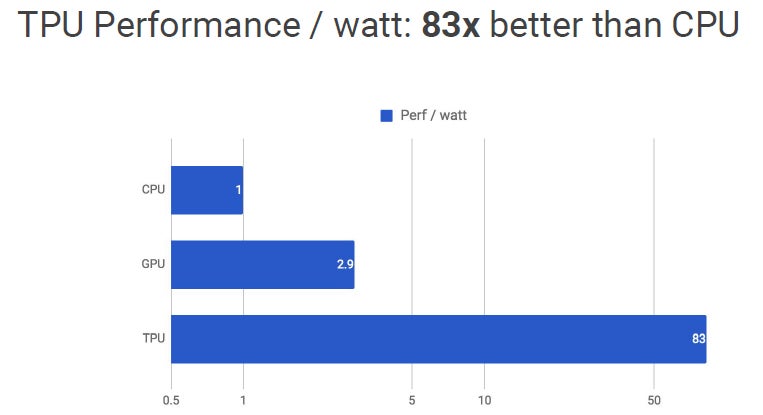
次の図はCPU、GPUとTPU v1の性能/Wを比較したもので、多分Haswell CPUとK80 GPUとの比較と思われる。CPUを1とすると、GPUは2.9倍、TPU v1は83となっており、圧倒的にTPUの性能/Wが高いことが分かる。

  • CPU、GPUとTPU v1との性能/Wの比較

    CPU、GPUとTPU v1との性能/Wの比較。TPU v1はCPUと比べて83倍の性能/Wである

次の図は、7msの応答時間のリミットでどれだけのスループットが得られるかという性能を比較したものである。前述のMLP0/1、LSTM0/1、CNN0/1それぞれのスループットを比較したものが右側の棒グラフで、TPU v1はCPUと比較してMLP0では41倍、MLP1では18.5倍の性能が得られている。CNNでも性能差は大きく、CNN0では40.3倍、CNN1では71倍となっている。一方、LSTM0では3.5倍、LSTM1では1.2倍と改善効果は、MLPやCNNと比べると小さい。

左の棒グラフは6種のアプリケーションを総合した比較で、CPUのスループットが5,482、GPUが13,194に対して、TPU v1は225,000であり、CPUの41倍、GPUの17倍と圧倒的に高いスループット性能となっている。

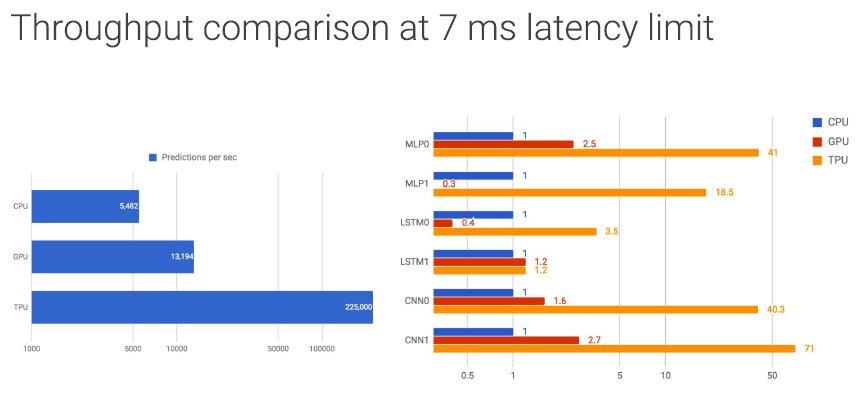
  • 7ms以内の応答という条件でのスループットの比較

    7ms以内の応答という条件でのスループットの比較。右はMLP0/1、LSTM0/1、CNN0/1それぞれの比較。左は6種のアプリケーションを総合した比較で、CPUが5,482、GPUが13,194に対して、TPU v1は225,000と圧倒的に高い性能となっている

次の図は、それぞれの機能のチップ上の配置を模式的に描いた図である。積和演算器アレイが24%の面積、それに入力データを供給するユニファイドバッファが29%の面積を占めており、この2つのユニットで全チップ面積の53%を占めている。

さらに、アレイの出力を足しこむアキュムレータが6%、マトリクス乗算の結果に非線形関数を適用するアクティベーションパイプラインが6%、DDR3 DRAMポートが左右の合計で6%などとなっている。一方、コントロールロジックは2%と小さく、制御論理的には単純な作りになっていることが分かる。

TPU v2は第2世代のTPUで、演算を16ビット浮動小数点数で行うことにより、推論だけでなく、学習も実行できるユニットとなっている。

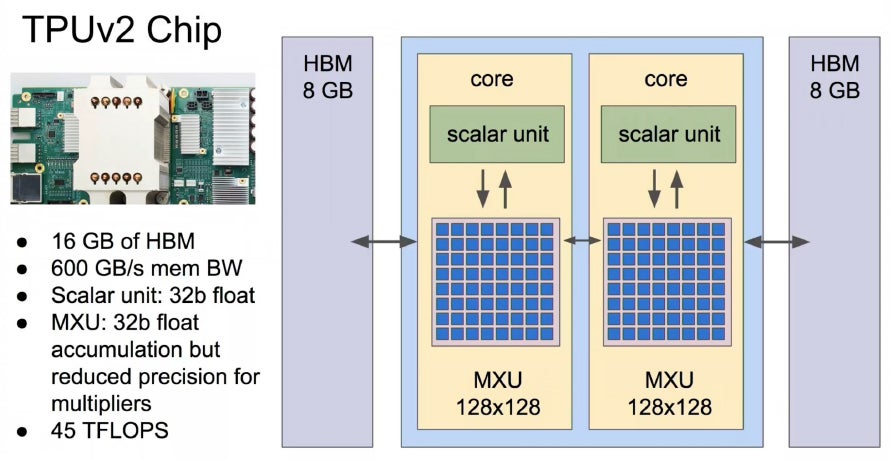
次の図の白い大きな放熱フィンが付いているのがTPU v2チップで、4個のTPU v2チップを1枚のプリント基板に搭載し、このボードをTPU v2と呼んでいる。TPU v2チップの最大演算性能は45TFlopsであり、ボードの性能は180TFlops、64枚のTPU v2を搭載するポッドの性能は11.5PFlopsとなる。

  • TPU v2は4個のチップを搭載したボードとなっている

    TPU v2は4個のチップを搭載したボードとなっている。チップ1個の性能は45TFlopsで、64枚のボードを搭載するPodは11.5PFlopsの演算性能を持つ

TPU v1からTPU v2への変更点

TPU v2が、作りの点でTPU v1から大きく変わっているのは、重みを格納するDRAMがHBMとなったことである。TPU v1の論文の性能分析では、外部のDRAMチップからのデータ読み出しのバンド幅が最大の性能ネックとなっていると書かれており、TPU v2ではHBMの採用で、このボトルネックを解消している。

もう1つの大きな違いは、マトリクス乗算がTPU v1では8bit整数で演算していたが、TPU v2では学習にも使えるように浮動小数点数での演算に変わった点である。浮動小数点演算器は整数演算器に比べてトランジスタ数が多く、チップ面積も多く必要となるため、256×256個は搭載できず、TPU v2では128×128が2組となったと思われる。

しかし、マトリクス乗算器アレイの一辺の長さは2のベキにする必要は無く、180×180程度で1つのアレイとしても良かったはずである。多少であるが、この方がアキュムレータなどは減らせる。なぜ、このような128×128アレイを2組にしたのかと発表者に質問したのであるが、チップの開発には携わっておらず、理由は分からないという答えであった。

  • TPU v2チップの概要とブロック図

    TPU v2チップの概要とブロック図

これまで、マトリクスの積の入力は低精度浮動小数点数と書かれているだけで具体的なフォーマットは発表されていなかったが、今回の発表では、次の図のようなBrain Floating Point Formatという数値表現形式を使っていることが明らかにされた。

次の図の一番上は32bit長のIEEE規格の単精度という形式、2番目は16bit長のIEEE規格の半精度という形式である。半精度は符号1bit、指数部5bit、仮数部10bitとなっている。これに対してTPU v2チップでは図の一番下のbfloat16というGoogle独自の形式を使っている。bfloat16はデータの全長は16bitで半精度と同じであるが、指数部が8bitで仮数部が7bitとなっている。半精度と比べると数値の精度は低いが、数値の範囲は広いという設計である。

これはニューラルネットワークの計算では、精度は8bit(符号1ビットと仮数7ビット)でTPU v1の整数計算と同じ精度があれば良く、数値の範囲を決める指数部は8ビットを確保してIEEE単精度と同じ範囲の数を扱えるようにするのが良いという考え方で決められたと考えられる。

  • 浮動小数点数のフォーマット

    浮動小数点数のフォーマット。上からIEEE754の単精度fp32、IEEE754の半精度fp16、そしてGoogle独自のBrain Floating Formatと呼ぶbfloat16フォーマット。TPU v2ではbfloat16を使っている

TPUを外部ユーザーが活用するためには?

GoogleはTPUを外販していないが、社外にもクラウドでTPUを使わせるクラウドTPUというサービスを行っている。現在、TPU v2の1時間の使用料は6.50ドルである。

次の写真のBとCと書かれた中央の2つのラックはTPU v2のラックで、4個のTPU v2チップを搭載したTPU v2ボードが合計64枚搭載されている。左右のAとDのラックは、TPU v2を制御し、入出力のデータのやり取りなどを行うCPUなどが収容されていると思われる。

  • 64枚のTPU v2ボードを搭載するTPU v2ポッドの外観

    64枚のTPU v2ボードを搭載するTPU v2ポッドの外観

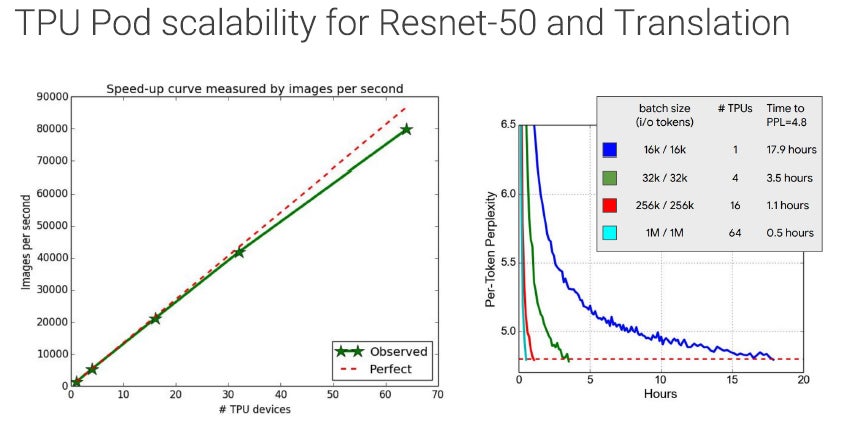
次の図の左のグラフはRenet-50でのイメージ認識の性能を示すもので、横軸は使用するTPU v2の台数で、縦軸はイメージ認識のイメージ数/秒の性能である。64TPU v2の場合でも、破線で示した理想的なケースに比べて性能低下は10%程度であり、かなり高いスケーラビリティが得られている。まあ、推論の場合はTPU間の通信はほとんどなく、分散処理ができるので、当然と言える。

右のグラフは翻訳の性能で、縦軸は翻訳の不確かさ、横軸は処理時間で4本のグラフはTPU数が1、4、16、64に対応している。不確かさが4.8に下がるまでの時間は、1TPUでは17.9時間掛かるが、64TPUを使うと0.5時間と約1/38になっている。推論よりはスケーラビリティが下がるが、まあ、良い結果と言える。

  • Resnet-50のイメージ認識性能と翻訳性能

    左はResnet-50を使ったイメージ認識性能、右は翻訳の性能のスケーラビリティを示す

ということで、Googleは8bit整数で大量の推論計算を行うTPU v1と、当初はNVIDIAのGPUを使っていた学習処理を自前で行うTPU v2を開発し、推論も学習も自社開発のTPUで実行できる体制を整えた。しかし、どちらも28nmプロセスを使っていると思われ、さらに高密度の16nm/14nm、時期によっては10nmかそれ以下のプロセスを使ってより高密度のTPUの開発が進められているのではないかと推測される。