ディープラーニングの基礎(6) - 勾配法による学習

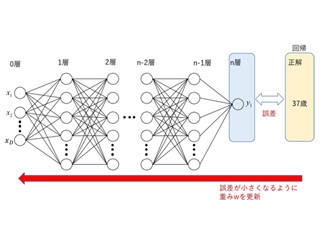
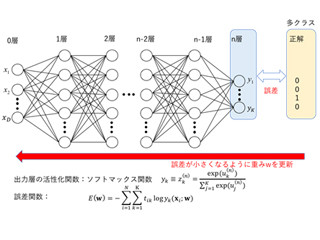
今回は、ディープラーニングの基礎の第6回目(基礎の第1回目はコチラ)です。ニューラルネットワークの学習の基礎知識である勾配法についてご紹介します。ディープラーニングの基礎の第3回となる本連載の第44回で説明した通り、教師データ(正解データ)と予測値との一致度を表す損失関数(誤差関数)を定義し、その損失関数が最小となる最適な重みパラメータとバイアスを自動的に求めます。この最適なパラメータを求めることが機械学習における学習です。このように教師データから問題を解くために必要なパラメータを自動的に求められることがディープラーニングを含む機械学習の大きなメリットと言えます。パラメータ数は数千、数万を超えるため、手作業で最適値を求めることはほぼ不可能ですので。

勾配法

ディープラーニングを含む多くの機械学習では、先述の損失関数が最小となる最適なパラメータを求めることになりますが、一般的に損失関数は非常に多くのパラメータを含むため複雑な形となります。シンプルな方程式を解くような線形解法では解けない場合がほとんどです。そこで勾配法と呼ばれる、損失関数がより小さくなるようなパラメータを繰り返し求めることで最適値を得る方法を用いることになります(図1)。重みパラメータw=w₁における損失関数の勾配を求め、その勾配を利用して損失関数の値がより小さくなるパラメータw₂を求めます。勾配を求める際に、高校や大学で勉強した微分、偏微分が登場しますので、忘れてしまったという方は復習しておいて下さい。

• 図1 勾配法

ニューラルネットワークにおける勾配法

図2に示すような、入力層のノードがそれぞれ10個、中間層のノードが20個、出力層のノードが5個のシンプルなネットワークを例に説明したいと思います。中間層のノードm₁の値を求めるために、入力層の全ノードからの入力値に対し重みw¹_(1,1),…w¹_(1,10)を掛けて総和を取りb¹₍₁₎を足すことになります。中間層のノードm₂の値を求めるためには、入力層の全ノードからの入力値に対し重みw¹_(2,1),…w¹_(2,10)を掛けて総和を取りb¹₍₂₎を足します。同様に、出力層のノードy₁の値を求めるためには、中間層の全ノードから出力層に入力される値に対し重みw²_(1,1),…w²_(1,5)を掛けて総和を取りb²₍₁₎を足します。

つまり、更新したい重みパラメータは入力層と中間層の間で10×20の200個、バイアスは20個となります。中間層と出力層の間は、重みパラメータが20×5の100個、バイアスは5個となります。これらの勾配を一度に計算することはできないため、1つのパラメータに着目しそれ以外のパラメータを固定する偏微分が必要となります。w¹_(1,1)を更新する場合は、w¹_(1,1)以外のパラメータを固定し以下の通り値を更新します。ただし、損失関数をL(w)とし、αはパラメータの更新量です。

• 図2 ニューラルネットワーク