中性子星合体後は超高圧状態の違いで重力波の周波数が異なる、理研などが予測

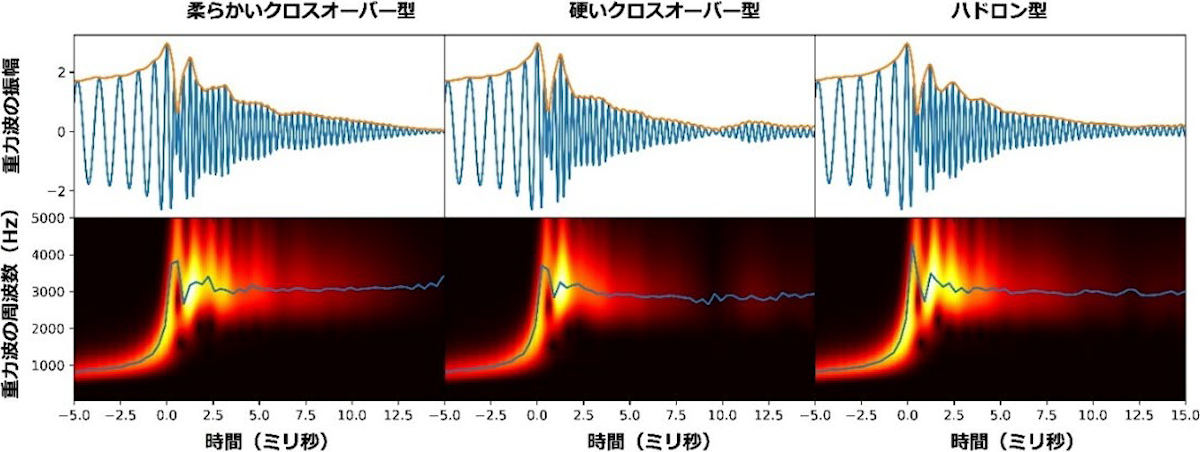
一般的に、物質の圧縮時に圧力上昇が大きいと「状態方程式が硬い」、逆に小さいと「状態方程式が柔らかい」と表現される。得られた重力波の詳細な解析から、合体中性子星がラグビーボールやダンベル形につぶれることで、放出される重力波の周波数が柔らかい、または硬いCO型状態方程式、ハドロン型状態方程式という3種類の特性をよく反映していることが確認されたという。

CO型状態方程式は、密度が核飽和密度の3倍程度では、ハドロン相だけで構成されるハドロン型状態方程式に比べて硬く、密度が核飽和密度の4倍程度を超えると柔らかくなるという特性があるという。

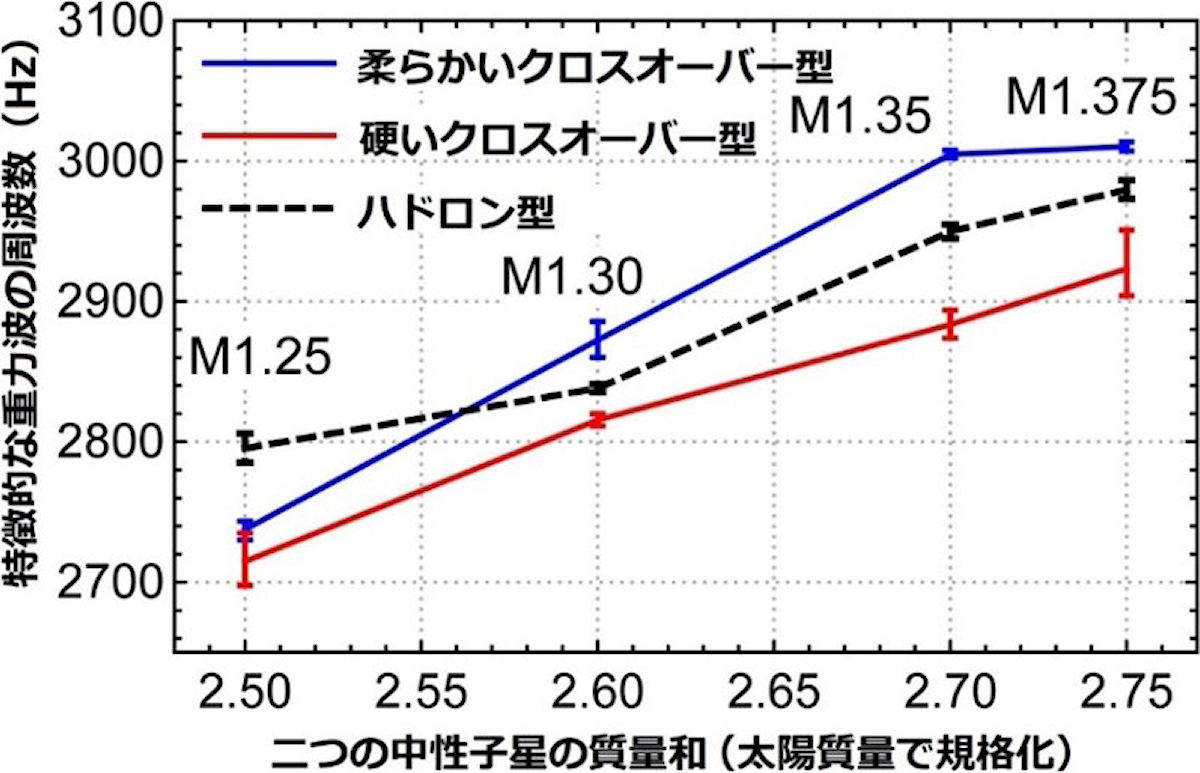
軽い中性子星同士による合体中性子星は比較的軽く、中心密度が核飽和密度の3倍程度に抑えられる際に多量の重力波が放出される。この場合、硬いCO型状態方程式で表される合体中性子星は半径が大きいため速い回転ができず、結果的に放出される重力波の周波数は低くなるという。

一方、重い中性子星同士による合体中性子星は比較的重く、中心密度が核飽和密度の4倍程度を超え、その際に多量の重力波が放出される。そのため、柔らかいCO型状態方程式で表される中性子星は半径が小さく、速く回転するため、放出される重力波の周波数は高くなる傾向にある。ただし、CO型状態方程式が核飽和密度の関数としてどれくらい硬くまたは柔らかくなるかは、現在の原子核理論では確定できず、不定性が残るとする。

そこで、CO型状態方程式が柔らかい場合と硬い場合の双方が調べられ、ハドロン型状態方程式との比較が行われたところ、軽い中性子星同士の合体では、硬いCO型状態方程式で表される合体中性子星は半径が大きくなり、重力波の周波数は柔らかい状態方程式の場合よりも低くなることが明らかにされた。

一方、合体中性子星が重くなってくると、特に柔らかいCO型状態方程式で表される合体中性子星の半径は小さくなり、重力波の周波数は高くなる。硬いCO型状態方程式で表される合体中性子星は、ハドロン型状態方程式の場合に比べて半径が大きく保たれたままで、重力波の周波数は低めに抑えられていることがわかった。

異なる状態方程式に対する連星中性子星合体時の重力波波形とスペクトル (出所:理研Webサイト)

これらの結果から、ハドロン-クォーク連続性に伴う重力波の特性は、密度とともに単調に硬くなるハドロン型状態方程式(ハドロン物質のままとどまる)や、クォーク物質が現れると一気に柔らかくなる従来の一次相転移型状態方程式(ハドロン物質が一次相転移を経て、クォーク物質が突然現れる)に伴うものとは明らかに異なることが確認されたと研究チームでは説明する。

なお、今回提案された周波数帯(約3kHz)の重力波の検出は現状では難しいが、米国のLIGOはアップグレードを予定しており、さらには次世代の重力波検出器の建設計画も欧米を中心に進む。そのため、2030年代には連星中性子星の合体後の特徴的な重力波が次々と観測される可能性があり、そうした観測から、中性子星内部の超高圧化でクォーク物質が現れるのか、現れるとすればどのようにハドロン物質からクォーク物質への変化が起きるのかといったことの理解が進むことが期待されるとしている。