割り算の教科書をみると、引き戻し法では最大2Nサイクルを必要とするが、引き放し法では、最大N+1サイクルで計算ができるので、引き放し法の方が速いと書いてある。しかし、引き算の結果がマイナスになったからといって、元に戻すだけのために次の1サイクルを使うような設計は良い設計とは言えない。仕事でこんな設計をしていたのでは、上司にお目玉を食らうのが関の山である。
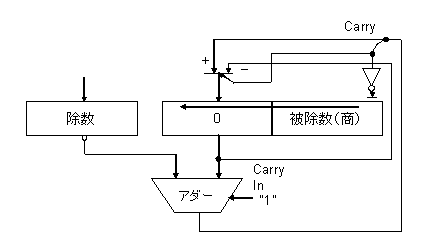
引き過ぎを戻すのに1サイクルを使わないでも、次の図のように、アダーの出力がマイナスになったら、被除数レジスタに引き算結果を書き込むのではなく、もとの被除数レジスタの値を書き込めば、同一サイクルで引き戻すことができる。
 |
|
図5:改良型の引き戻し法割り算器。減算結果がマイナスになると、アダーを通す前の被除数を書き戻す。 |
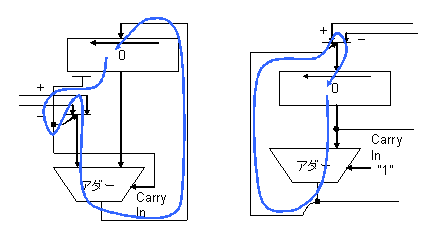
このようにすると、被除数レジスタの前にマルチプレクサが必要となるが、実は、前に掲げた図2の回路でもアダーの加算と減算を切り替えるには、除数とその否定を切り替えるマルチプレクサが必要なので、特に部品が増えるわけではない。また、次の図6に両方の割り算器のクリティカルパス(サイクルタイムを決める、遅延時間的に一番長いパス)を青線で示すが、どちらの方式も被乗数レジスタ、マルチプレクサの切り替え入力からデータ出力、アダーを通っており、サイクルタイム的にも差がない。
 |
|
図6:割り算器のクリティカルパス。左が図2の方式で除数の加算、減算の切り替えのマルチプレクサがある。右が同一サイクルで戻す方式。 |
つまり、図6右の回路を使えば、引き戻し法でもNサイクルで割り算ができ、1サイクルの長さの点でも図2の回路と差がないので、引き放し法よりも、若干、速く割り算ができてしまう。
ゼロをスキップして計算時間を短縮
また、割り算の最初は、被除数レジスタの上位半分はゼロが詰まっており、除数を引くと、当然、マイナスになってしまう。この状態は、割り算ステップが進んで被除数が左シフトされて、被除数の最上位ビットの位置と除数の最上位ビットの位置が一致するまでは続く。引き戻し法の場合でいうと、この状態になるまで、引き算をやって、それを戻すという操作を繰り返しているだけで無駄である。
整数の割り算の場合は、普通のプログラムでは、被除数の値も32ビットとか64ビットの語長を一杯に使うような値が出現するのはまれなので、乗算のところでやったように、ゼロが連続していれば複数ビットの左シフトをまとめて1サイクルに行い、被除数の上位のゼロをスキップしてしまえば処理時間を短縮できる。
除数の最上位の"1"と並ぶ位置まで被除数の左シフトを繰り返すのがベストであるが、長い語のどこに最上位の"1"があるかを1サイクルで見つけるのには多くのゲートを必要とするし、更に、両者の最上位ビット位置の差に応じて任意のビット数の左シフトを行う回路も多くのゲートを必要とする。ということで、実用的には、被除数レジスタの下側半分の最上位側の数ビットを検査し、それが全てゼロの場合は、その部分が上位半分に入ってきても除数を超えることは無いので、検査したビット数分の左シフトを行うという方法が一般的である。
例えば、32ビットの被除数の上位16ビットがゼロであるとすると、単純な引き戻し法では32サイクル掛かるが、1サイクルに2ビットづつゼロスキップを行うと、8+16=24で24サイクルとなり25%速くなる。