本連載ではこれまで 8 回にわたって、全探索・二分探索・貪欲法・動的計画法といったアルゴリズムを紹介しました。今回は少し趣向を変えて、アルゴリズムを使って解ける数理パズル的な問題を 1 つ紹介します。
プログラミングを知らない人でも楽しめるものになっているので、ぜひ、より効率良く問題を解く手順を自力で考えてみてください。
アルゴリズムパズルに挑戦!
机の上に 5 個のおもり A・B・C・D・E が置かれています。あなたは 1kg・2kg・3kg・4kg・5kg のおもりが 1 個ずつあることを知っていますが、それぞれのおもりの重さを知りません。「2 つのおもりを天秤に乗せ、重さを比較する」という操作をできるだけ少ない回数行うことで、全てのおもりの重さを特定してください。
比較回数に制限がなければ、重さを特定すること自体はそれほど難しくありません。しかし、一番少ない比較回数で重さを特定するには、どうしたらよいでしょうか。以降では、ヒントになる考え方を説明していきます。
10 回で必ず当てる方法
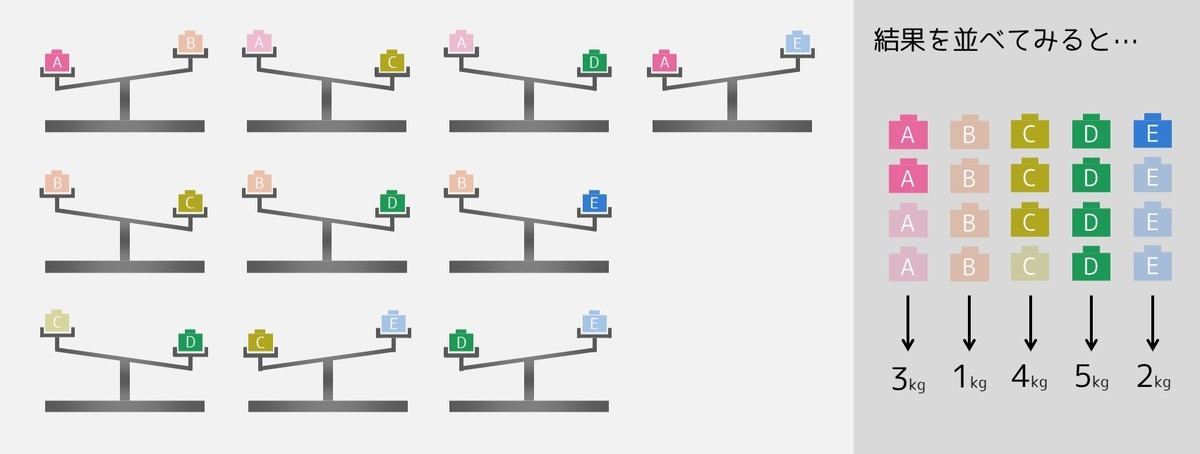
まずは一番分かりやすい「10回で当てる方法」について見ていきましょう。この場合、全てのおもりのペア(全部で 10 通りあります)について、天秤で重さを比較することを考えます。このとき、各おもりが 4 回ずつ比較され、以下のようになるため、全てのおもりの重さを特定することができます。
- 4 回中 0 回について「重い方」だった場合、そのおもりの重さは 1kg
- 4 回中 1 回について「重い方」だった場合、そのおもりの重さは 2kg
- 4 回中 2 回について「重い方」だった場合、そのおもりの重さは 3kg
- 4 回中 3 回について「重い方」だった場合、そのおもりの重さは 4kg
- 4 回中 4 回について「重い方」だった場合、そのおもりの重さは 5kg
下図はその具体例です。なお、同じような方法を使うと、n(n-1)/2 回の比較で n 個のおもりを軽い順に並べ替えることが可能です。
9 回で必ず当てる方法
前述の方法を工夫し、次のような手順で比較を行うと、合計比較回数が 3+2+4=9 回となります。
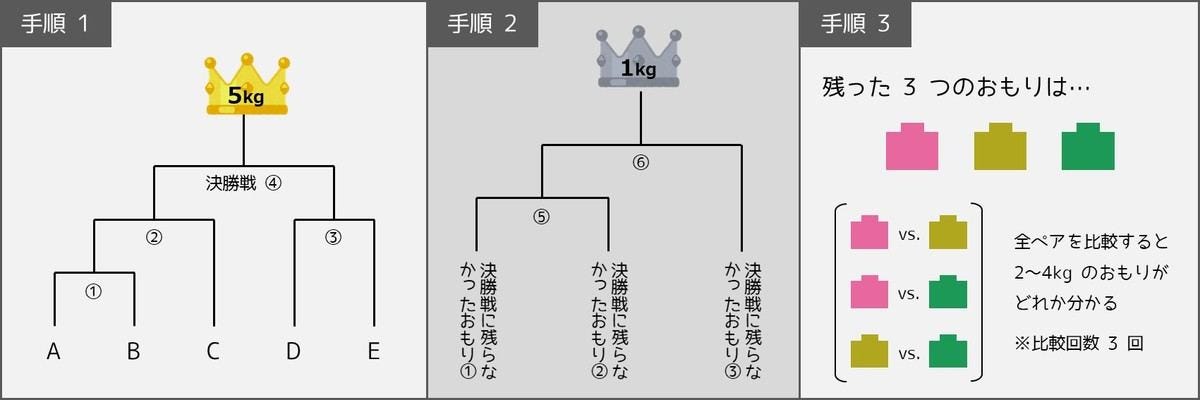
- 手順1: 下図の [手順1] のようにして、A~E の中で一番重いものを 4 回の比較で求める。
- 手順2: 下図の [手順2] のようにして、A~E の中で一番軽いものを 2 回の比較で求める。
- 手順3: 残りのおもりのペア(3 通りあります)を全て比較することで、2kg・3kg・4kg のおもりがどれであるかを特定する。
なお、手順1 の 4 回目の比較で使用されたおもりは「少なくともどれか1つよりは重い」ということがすでに分かっています。そのため、最も軽いおもりを求める手順2 では候補から外してもかまいません。
8 回で必ず当てる方法
続いて8回で当てる方法を説明しますが、その前に、まずは次の問題について考えてみましょう。
机の上に n-1 個のおもりが軽い順に並べられている状況を考える。そのとき、残り 1 つのおもりをどこに挿入すれば n 個全部が軽い順に並べられるかを求めよ。
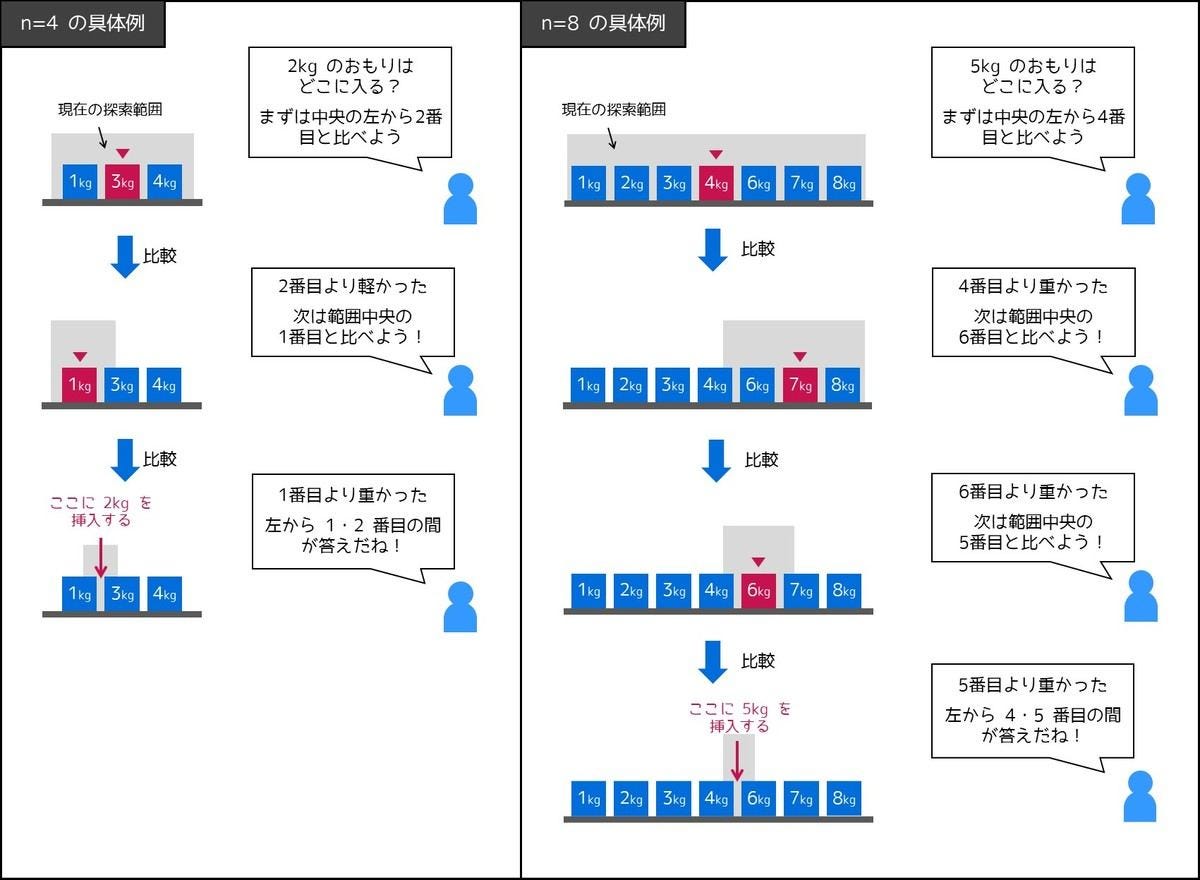
例えば左から順に [1kg, 3kg, 4kg] のおもりが並べられていて、2kg のおもりが残っているとき、左から 1 番目と 2 番目の間に挿入すれば良い。
少し難しいですが、第 4 回 で扱った二分探索法を使うと、最大 ⌈log2 n ⌉ 回の比較で挿入位置を求めることができます。特に、n = 1, 2, 3, 4, 5 の場合の比較回数は次表の通りです。
| n | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 比較回数 | 0 | 1 | 2 | 2 | 3 |
ここで、次のような手順で比較を行うと、8 回で確実に当てることができます。なお、机には「軽い方が左になるようにする」というルールを保ったまま、1 つずつおもりが追加されていくものとします。
- 手順1: 最初、おもり A だけを机に置く。
- 手順2: おもり B を適切な位置に挿入する。挿入位置は⌈log2 2 ⌉ = 1 回の比較で分かる。
- 手順3: おもり C を適切な位置に挿入する。挿入位置は⌈log2 3 ⌉ = 2 回の比較で分かる。
- 手順4: おもり D を適切な位置に挿入する。挿入位置は⌈log2 4 ⌉ = 2 回の比較で分かる。
- 手順5: おもり E を適切な位置に挿入する。挿入位置は⌈log2 5 ⌉ = 3 回の比較で分かる。
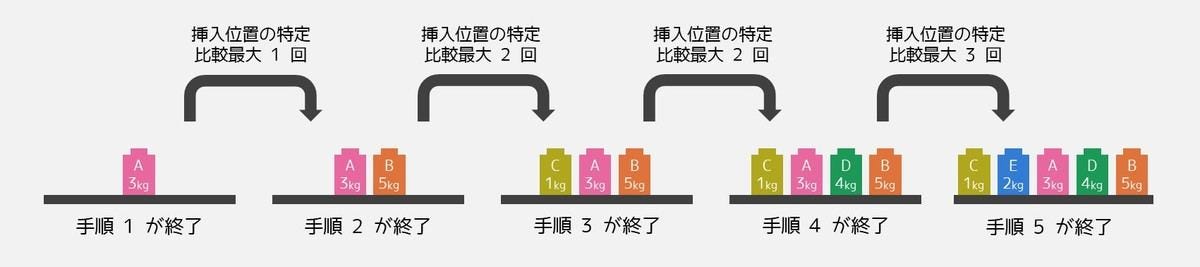
下図は、おもり A・B・C・D・E がそれぞれ 3kg・5kg・1kg・4kg・2kg であった場合における、机の上の変化を示しています※。
7 回以内で当てる方法
最後に、この問題は 6 回で確実に当てることが不可能である一方、7 回は可能であることが知られています。手順が非常に複雑で説明が長くなるため、本稿では割愛しますが、詳しく知りたい方は筆者がGitHubで公開している 「アルゴリズム×数学」節末問題 5.10.7 (1) の解説 をご覧ください。
* * *
次回からは 2 回に分けて、データの集まりを上手く管理するためのデータ構造について説明します。データ構造は、高度なアルゴリズムを支える重要な概念です。ぜひ楽しみにお待ちください。
※同じような方法を使うと、およそ n log2 n 回の比較で n 個のおもりを軽い順に並べ替えることが可能です。