動的計画法（その 2 ）：ナップザック問題

第7回では、一次元配列を用いて動的計画法を適用させる問題を 2 つ紹介しました。この考えを二次元配列にも拡張させると、動的計画法の応用範囲はぐっと広がります。今回は、動的計画法の実用的な例として、「ナップザック問題」とその解法について解説します。

第7回「動的計画法（その 1）」はこちらから

ナップザック問題とは

次のような問題をナップザック問題と言います。

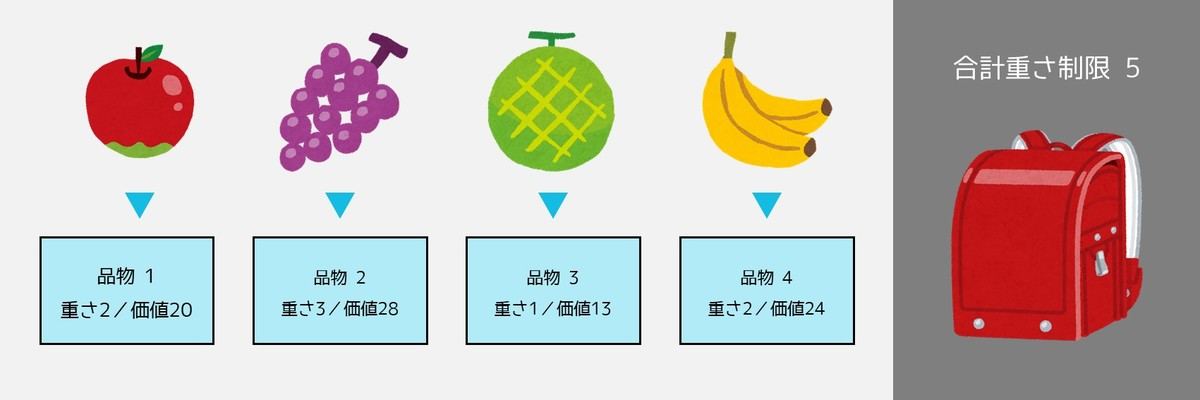
N 個の品物があります。i 番目 (1 ≤ i ≤ N) の品物の重さは w_i で、価値は v_i です。重さの合計が W 以下となるように品物をいくつか選ぶとき、どのように選べば価値の合計が最大になりますか。

制約： 1 ≤ N ≤ 100、1 ≤ W ≤ 10⁵、1 ≤ w_i ≤ W、1 ≤ v_i ≤ 10⁹

実行時間制限： 2 秒

出典： アルゴリズムと数学 演習問題集 030 - Knapsack 1

例えば、下図のようにN (=4) 個の品物があり、重さの制限がW (=5) であるとします。このとき、品物 1・3・4 を選ぶと合計価値は 20+13+24=57 となり、これが最適です。それでは、スマートに答えを求める方法を考えてみましょう。

解法 1：全探索

まず思いつくのは、品物の選び方を全探索^※することです。確かにこの方法でも、 N が小さい場合は比較的簡単に解くことができます。例えば N=4 では 2⁴ = 16 通りしか調べる必要がなく、手計算でも十分現実的です。

しかし、品物の数 N が大きくなると組み合せ爆発を起こし、コンピューターを使っても現実的な時間内で答えを出すことができません。例えば N=60 の場合は 2⁶⁰ 通り、すなわち約 115 京通りという、膨大な数を探索する必要があります。では、一体どうすれば良いのでしょうか。

※ 全探索については、本連載の第２回で紹介しています。

解法 2：動的計画法

ナップザック問題は、次のようなアルゴリズムで高速に解くことができます。

ステップ 1｜二次元配列の定義

まず、二次元配列 dp を用意します。dp[i][j]は、品物 1, 2, …, i の中から重さの合計がちょうど j になるように選んだときの、合計価値として考えられる最大値を表します。

ステップ 2｜値の計算に関する考察

品物 1, 2, …, i までの中からいくつかの品物を選んだとき、重さの合計が j になるための条件を考えます。最後の行動で場合分けをすると、次のようになります。

• 品物 i を選ぶ： 品物 1, 2, …, i-1 の中からいくつか選んだとき、重さの合計は j-w_i
• 品物 i を選ばない： 品物 1, 2, …, i-1 の中からいくつか選んだとき、重さの合計は j

ここで、品物 i を選んだ場合の合計価値の最大値は dp[i-1][j-w_i]+v_i、選ばない場合の合計価値の最大値は dp[i-1][j] と表せます。なお、j ≥ w_i でなければ品物 i は選べないことに注意してください。

ステップ 3｜値の計算

ステップ 2 の考察を踏まえ、次の式に従って i=1, 2, …, N の順に二次元配列を埋めていきましょう。求める答えは dp[N][0], dp[N][1], …, dp[N][W] のうち一番大きい値となります。

• j < w_i の場合： dp[i][j] = dp[i-1][j]
• j ≥ w_i の場合： dp[i][j] = max(dp[i-1][j],dp[i-1][j-w_i]+v_i)

具体例で考えてみよう！

抽象的な説明だけでは分かりづらい点もあるかと思いますので、冒頭で挙げた４つの品物の例をベースに、二次元配列を埋めてみましょう。まず、i=0 のときは「何も選ばない」という選択肢しかないので、dp[0][0]=0 です。dp[0][1] など選び方が存在しない部分については、便宜上「－」と記しています。

次に、i=1 のときは以下のように計算することができます。なお、以下の2つ目の式について、dp[0][2] の値は「―」となっていますが、非常に小さい値だと見なしても計算結果に影響はありません。

• 0 < w₁ なので、dp[1][0] = dp[0][0]=1
• 2 ≥ w₁ なので、dp[1][2]=max(dp[0][2], dp[0][0]+20)=20

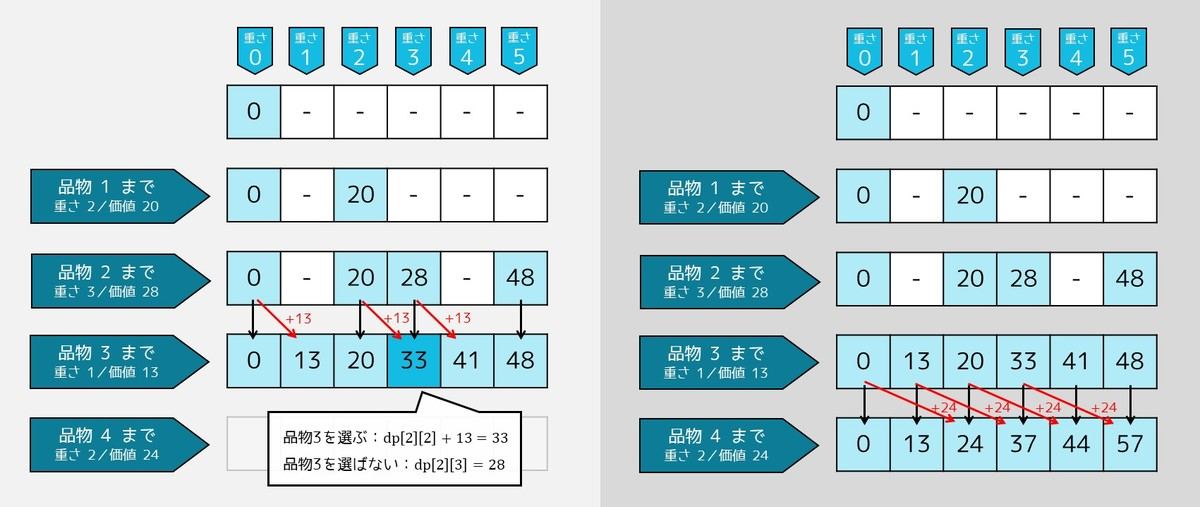
i=2 の場合も同じように計算すると、下図のようになります。

i=3, 4 の場合も同じように計算すると、下図のようになります。ここで、合計価値の最大値は dp[4][0], dp[4][1], …, dp[4][5] のうち一番大きい値なので、答えは 57 です。全探索で求めた値と確かに一致しています。

ナップザック問題の実装

以上のアルゴリズムを Python で実装すると次のようになります。1 ≤ i ≤ N、0 ≤ j ≤ W の範囲でループをしているため、計算量は O(NW) であり、N=100, W=100000 のような大きい入力でも一瞬で解くことができます。

なお、図で「－」と記された部分については、-10¹⁸ などの非常に小さい値を設定しておけば、「－」であるかどうかに応じた場合分けをせずに実装することが可能です。

# N, W, w[i], v[i] の設定（実際は入力をする必要があります）
N = 4
W = 5
w = [2, 3, 1, 2]
v = [20, 28, 13, 24]

# 配列の初期化
INF = 10 ** 18
dp = [[-INF] * (W+1) for i in range(N+1)]
dp[0][0] = 0

# 動的計画法
for i in range(1, N+1):
    for j in range(0, W+1):
        if j < w[i]:
            dp[i][j] = dp[i-1][j]
        else:
            dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]] + v[i])

# 出力
print(max(dp[N]))

発展：最適解の構成を求める

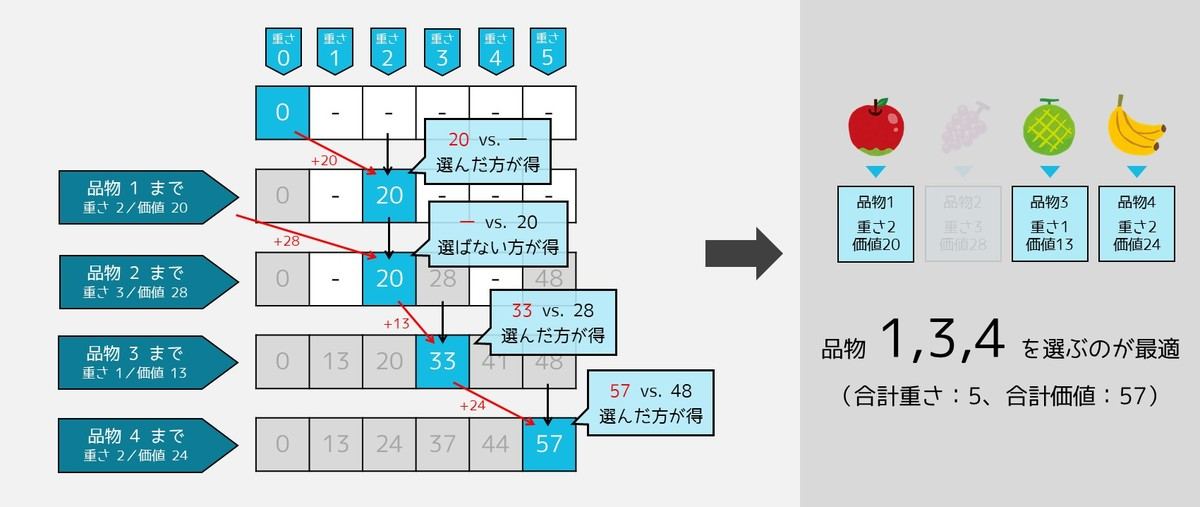
最後に、合計価値の最大値だけでなく、「具体的にどう選べば最大になるのか」を求めてみましょう。少し難しいですが、品物 4 → 3 → 2 → 1 の順に逆から考えると上手くいきます。

まずは品物 4 について調べてみましょう。品物 4 までの中から重さが 5 となるように選ぶ方法は以下の 2 つがあり、そのうち合計価値が dp[4][5]（=57） と一致するのは前者であるため、品物 4 は選んだ方が良いと言えます。

• 品物 4 を選ぶ場合：合計価値は dp[3][3] + 24 = 57
• 品物 4 を選ばない場合：合計価値は dp[3][5] = 48

次は品物 3 について調べてみましょう。品物 3 までの中から重さが 3 となるように選ぶ方法は以下の 2 つがあり、そのうち合計価値が dp[3][3]（=33） と一致するのは前者であるため、品物 3 は選んだ方が良いと言えます。

• 品物 3 を選ぶ場合：合計価値は dp[2][2] + 13 = 33
• 品物 3 を選ばない場合：合計価値は dp[2][3] = 28

下図のように、品物 2、品物 1 にも同様の計算を行うと、品物 1・3・4 を選ぶのが最適であることが分かります。

今回は、動的計画法の応用編としてナップザック問題について考えてみました。全探索では膨大な時間がかかる問題も、動的計画法を使えば素早く解ける可能性があります。計算回数が多くなりそうな問題に出会った際は、ぜひこのアルゴリズムも思い出してみてください。