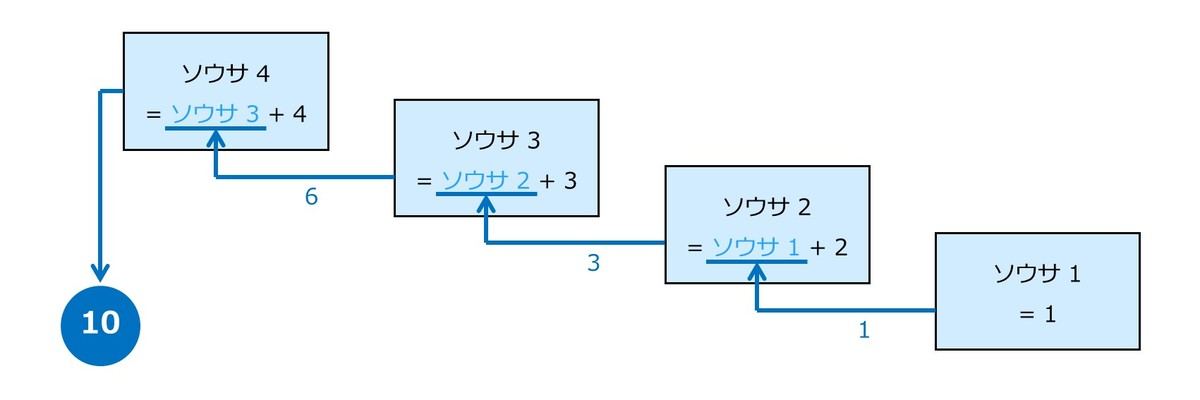
Let’s 競技プログラミング! E8さんが教えるアルゴリズム発想のキホン(10) 再帰関数とは?

早速ですが、次のような問題を考えてみましょう。「ソウサ 4」の結果はいくつになるでしょうか。

ソウサ x：

x=1 のとき、ソウサ x の結果は 1 である。

x ≥ 2 のとき、ソウサ x の結果は「ソウサ x-1 の結果に x を足した値」である。

答えは下図の通り 1+2+3+4=10 になります。

さて、この例では答えを求めるために「ソウサの結果」を呼び出しており、このように自分自身を引用することを「再帰的定義」と言います。また、プログラミングにおいて自分自身を呼び出す関数を「再帰関数」と言います。再帰関数は、複雑なアルゴリズムを簡潔に実装するときに便利なツールである一方、初学者にとっては最初の壁になりがちです。そこで今回は、3 つの例を用いてわかりやすく解説していきたいと思います。

再帰関数の例 (1)：足し算

冒頭の例を Python で実装すると次のようになります。元々は「ソウサ x」だったのが sousa(x) になったと考えるとイメージしやすいと思います。

# sousa(x) は自分自身を呼び出す「再帰関数」
def sousa(x):
    if x == 1:
        return 1
    return sousa(x-1) + x

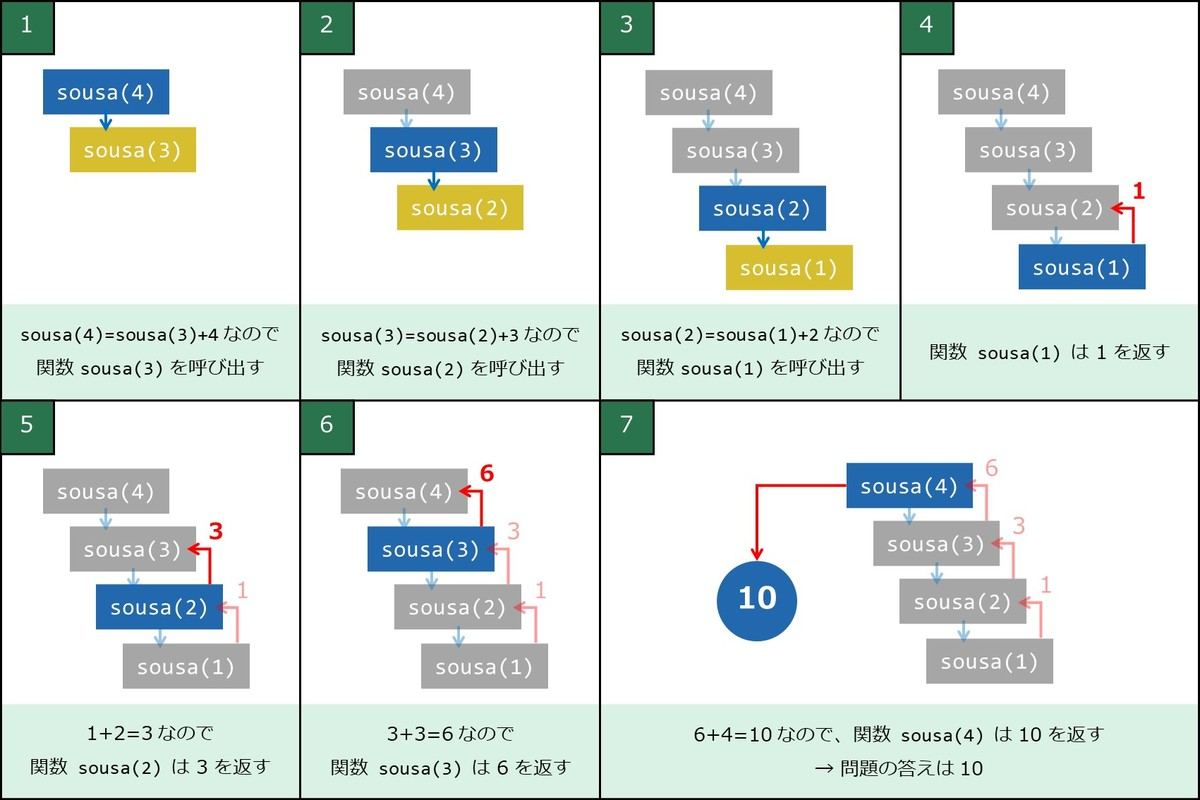
下図は、sousa(4) を呼び出した場合の挙動のイメージを表しています。返り値は前述の「ソウサ 4」と同じ 10 です。

再帰関数の例 (2)：フィボナッチ数列

次に紹介する例は「フィボナッチ数列」です。フィボナッチ数列は「第 1 項・第 2 項が 1 で、それ以降は前の 2 つを足した値」となるような数列のことを指し、第 10 項までは以下のようになります。

n	1	2	3	4	5	6	7	8	9	10
第 n 項	1	1	2	3	5	8	13	21	34	55

さて、フィボナッチ数列の第 n 項を求めるにはどうすれば良いのでしょうか。本連載の第 7 回・第 8 回で紹介した動的計画法を用いて計算することも可能ですが、今回は再帰関数を利用してみましょう。

def fib(n):
    if n <= 2:
        return 1
    return fib(n-1) + fib(n-2)

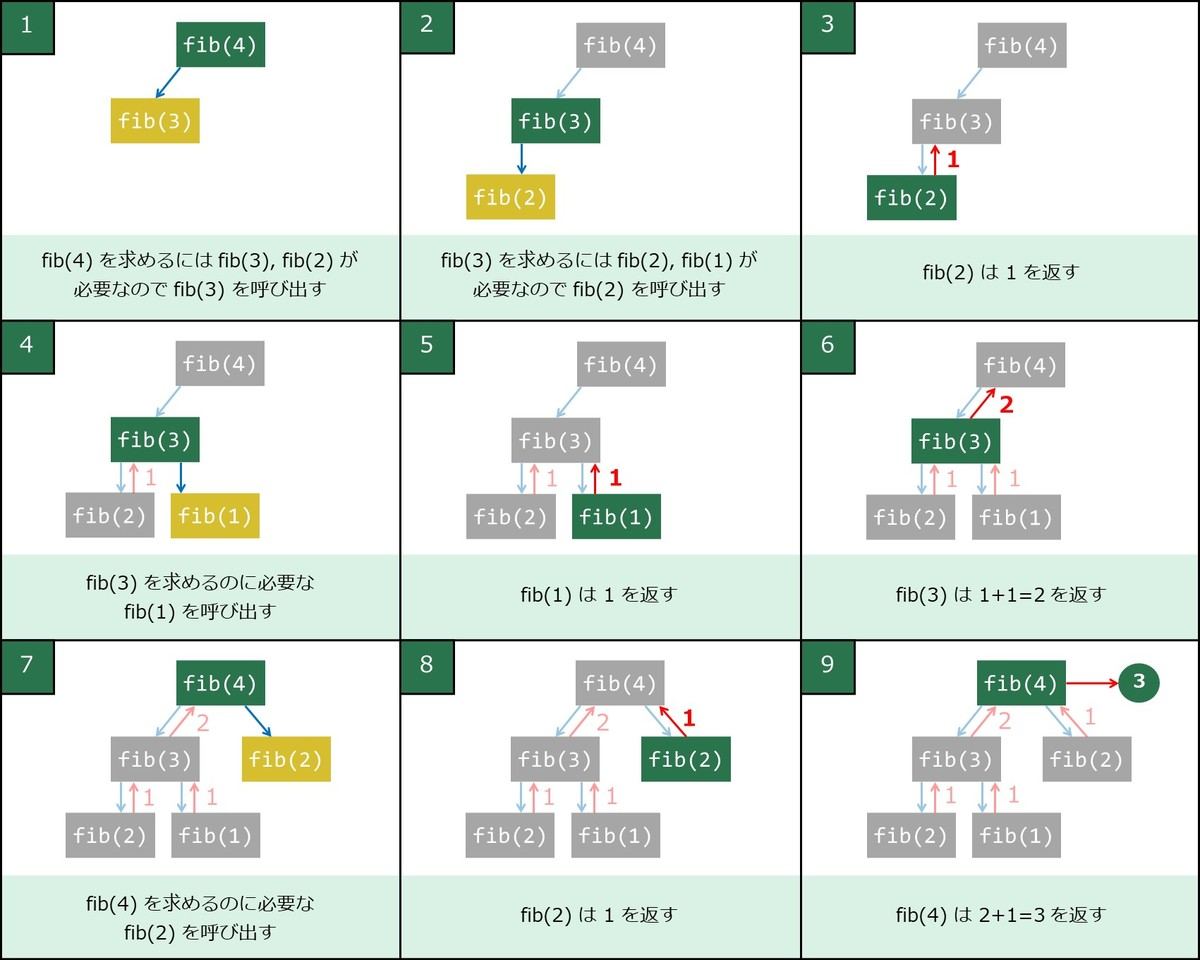
下図は、fib(4) を呼び出した場合の挙動のイメージを表しています。少し複雑ですが、最終的な返り値は 3 です。なお、このプログラムは n に対して計算回数が指数関数的に増加するため、n ≥ 50 だと現実的な時間内に処理が終わらないことに注意してください。

第7回「動的計画法（その 1）」はこちらから
第8回「動的計画法（その 2 ）：ナップザック問題」はこちらから

再帰関数の例 (3)：文字列を全部出力

再帰関数のイメージは掴めたでしょうか。最後にやや難しい例として、「a と b から成る N 文字の文字列をすべて出力する」というケースを考えてみましょう。単純に for 文を用いて実装することも可能ですが、以下のようなプログラムになり、とても面倒です。もっとスマートなやり方はないのでしょうか。

# N = 1 のとき
if N == 1:
    for s1 in ['a', 'b']:
        print(s1)

# N = 2 のとき
if N == 2:
    for s1 in ['a', 'b']:
        for s2 in ['a', 'b']:
            print(s1 + s2)

# N = 3 のとき
if N == 3:
    for s1 in ['a', 'b']:
        for s2 in ['a', 'b']:
            for s3 in ['a', 'b']:
                print(s1 + s2 + s3)

# N = 4 のとき（以下略）
if N == 4:
    for s1 in ['a', 'b']:
        for s2 in ['a', 'b']:
            for s3 in ['a', 'b']:
                for s4 in ['a', 'b']:
                    print(s1 + s2 + s3 + s4)

ここで再帰関数を使うと、次に示すような短いプログラムで正しく出力することができます。ここで、引数 N は出力したい文字列の長さ、引数 cur_string は現在の文字列を意味し、cur_string に 1 文字ずつ追加することによって再帰呼び出しを行います。

def func(N, cur_string):
    if len(cur_string) == N: # 文字数が N に達した場合
        print(cur_string)
    else:
        func(N, cur_string + "a") # s の後ろに "a" を付けた文字列にする
        func(N, cur_string + "b") # s の後ろに "b" を付けた文字列にする

# func(N, "") を呼び出すと、N 文字の a, b から成る文字列がすべて出力される
func(2, "")

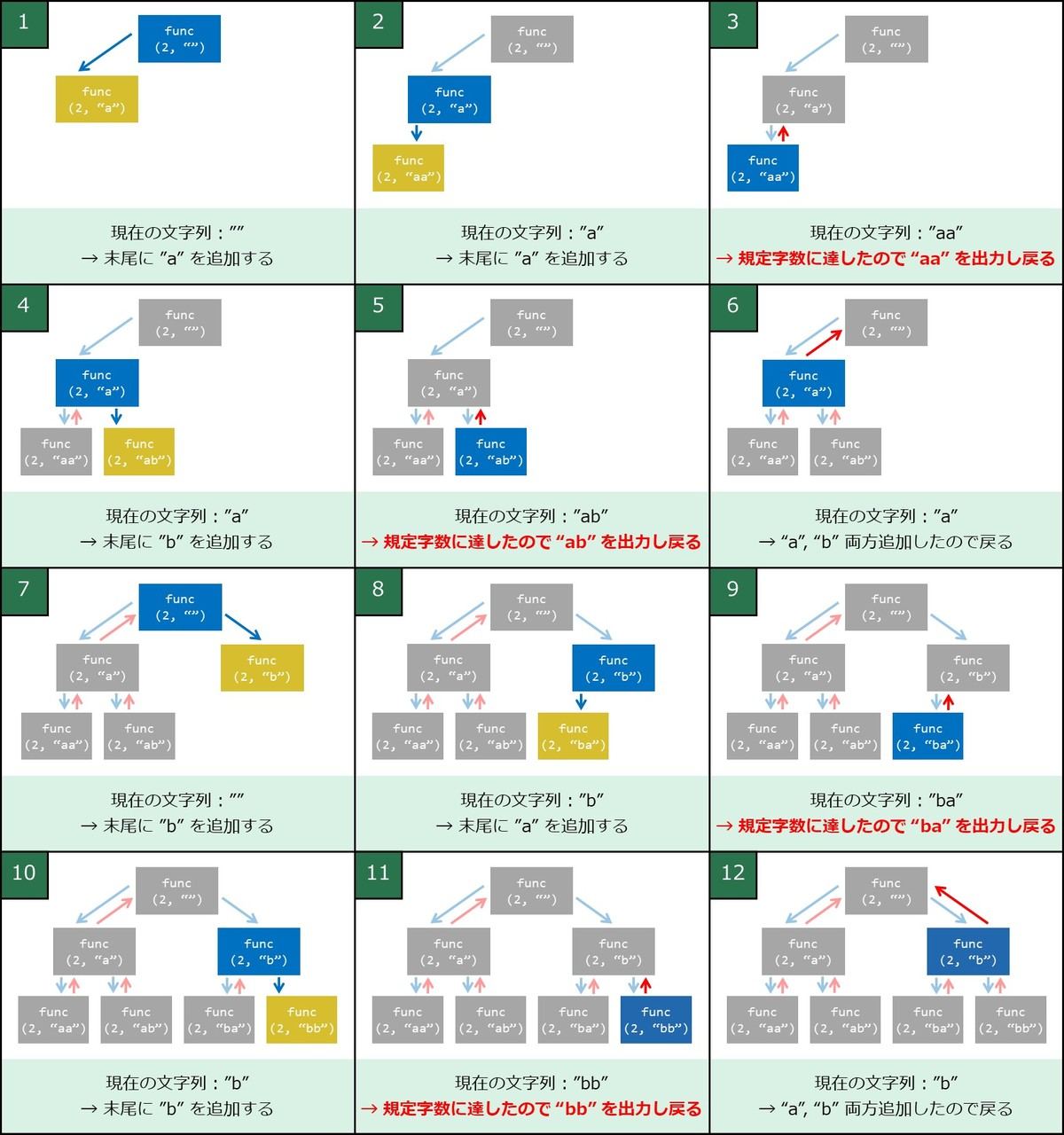
下図は、関数 func(2, "") を呼び出した場合の挙動のイメージを表しています。文字列はアルファベット順に出力され、N=2 のときは aa、ab、ba、bb の順になります。