早稲田大学(早大)と科学技術振興機構の両者は3月14日、量子計算機(量子コンピュータ)を現実世界の「組合せ最適化問題」に活用するためには、同問題が持つ制約を効率的に取り扱うことが重要であるとし、同問題を量子計算機で精度高く解くための新しい手法を開発。量子アニーリングマシンおよびゲート型量子コンピュータに適用して実際にその有効性を確認したことを共同で発表した。
同成果は、早大 理工学術院の白井達彦講師、同・戸川望教授らの研究チームによるもの。詳細は、IEEEが刊行する量子技術に関する全般を扱う学術誌「IEEE Transactions on Quantum Engineering」に掲載された。
実社会のさまざまなところに存在している組合わせ最適化問題は、大規模になるほど現行のコンピュータでは最適解を得ることが困難になるとされ、量子アニーリングマシンやゲート型量子コンピュータなどの量子計算機に期待が集まっている。
-
グラフ分割問題(2頂点)を例にした、今回の手法の概要。量子計算機から出力される解を、制約を満たす解に変換する制約適合処理手法を組み込んだ量子アルゴリズム(出所:早大Webサイト)
ただし、現在実用化されている量子計算機はノイズの影響に弱く(誤りを訂正する機能がない)、エラーなく実行できる時間が制限されてしまっており、短時間で計算可能な量子アルゴリズムを開発する必要があった。組合せ最適化問題を短時間の計算で解法する手法としては、これまで「変分法」を用いた量子アルゴリズムが開発されてきたが、"制約を持つ"組合せ最適化問題では、十分な精度を達成することは難しいという課題を抱えていたという。
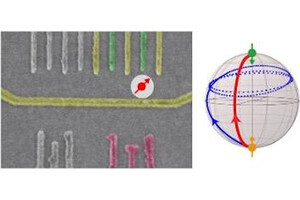
制約とは、たとえば2個の頂点を持つグラフを1個の頂点を持つ2個のグラフに分割する問題を考える場合などがある。この場合、各頂点について1個の量子ビットを対応させようとすると、当然2個の量子ビットが必要となる。制約とは、その2個の量子ビットのうち、一方は赤丸(0)、もう一方は青丸(1)とする必要があることをいう。
ところが、量子計算機は一般に制約を満たさない解を出力してしまうという。たとえば、2個の量子ビットの両方が赤丸(0)もしくは青丸(1)となるような解だ。このような制約を満たさない解は大きなエネルギー値を持つため、変分法を用いた量子アルゴリズムの精度を悪化させる要因となる。
そこで研究チームは今回、制約を満たさない解に対し、制約を満たす解に変換する制約適合処理手法を構築し、変分法と組み合わせることで、制約を持つ組合せ最適化問題を解くための量子アルゴリズムの構築を試みることにしたという。
制約適合処理手法により、制約を満たさない解を制約を満たす解に変換する場合、制約を満たす解空間において変分パラメータの最適化を行うため、精度高く組合せ最適化問題の最適解を探索できるとする。またこの手法は、量子アニーリングマシン、ゲート型量子コンピュータなど、量子計算機のタイプによらず導入できる点も特徴だという。そして今回の研究では、この手法が、実際にどちらでも有効であることも明らかにされた。
-
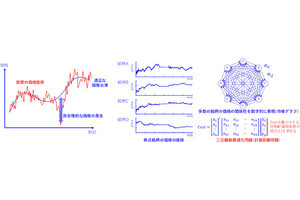
手法の比較。(左)量子アニーリングマシンによる実験結果。縦軸に今回提案された手法、横軸に従来手法が示されている(両軸共に、グラフ分割問題(32頂点および64頂点)を解いた時の残留エネルギーの平均値が表されている(0が最も精度が高い))。データが対角線の下側にあるということは、提案手法において従来手法よりも性能が改善していることが示されている。(右)ゲート型量子コンピュータを用いた実験結果。グラフ分割問題(4頂点)を解いた時の残留エネルギーの平均値が表されている(カッコ内は平均値の標準偏差が表されている)(出所:早大Webサイト)
この手法を用いて制約を持つ組合せ最適化問題を解くことを考える場合、制約を満たさないすべての解を、制約を満たす解に変換することのできる制約適合処理手法を構築することがポイントとなる。そこで今回の研究では、できる限り汎用的な制約適合処理手法を構築することを目指すことにしたとする。
まず、すべての局所最適解が制約を満たす解となるための条件が理論的に証明された。この条件が満たされる時、局所最適解を求めるための手法、たとえば「貪欲法」によって制約適合処理手法を構築することが可能。この条件は、独立な線形制約を持つ組合せ最適化問題に対して成立し、現実世界に現れる多くの組合せ最適化問題に対して適用できるとし、典型的な組合せ最適化問題に対して、具体的に今回の手法が適用可能であることが示されたとした。
次に、量子計算機ですら解法が困難とされる組合せ最適化問題の「グラフ分割問題」に対し、制約適合処理手法を組み込んだ場合(今回の手法)と組み込まなかった場合とが比較された。その結果、残留エネルギーを量子アニーリングマシンでは平均85％削減、ゲート型量子コンピュータでは平均87％削減し、得られる解の精度が改善されることが確認された。
今回の手法は量子計算機であれば容易に導入できることから、現在および近い将来に実現する量子計算機の性能を最大限引き出すための量子ソフトウェア開発の要素技術として利用されることが期待されるとした。研究チームは今後、一層広範囲な組合せ最適化問題への適用を進めながら、実世界に見られるさまざまな具体的な問題に対して、今回の手法の有効性を検証していくとしている。
