NIMS、高温超伝導体実現のカギとして「モット転移」近傍の謎を統一的に解明

物質・材料研究機構(NIMS)は2月15日、「電子相関」によって生じる絶縁体への「金属絶縁体転移(モット転移)」の本質を理論的に明らかにし、高温超伝導体で観測されているさまざまな「異常な振る舞い」をモット転移近傍の性質として統一的に説明することに成功したと発表した。研究はNIMS国際ナノアーキテクトニクス研究拠点(MANA)の河野昌仙研究者らの研究グループによるもので、成果は米物理学会の論文誌「Physical Review Letters」オンライン版に2月15日に掲載された。

金属中の電子は互いに反発しながら動いているが、電子の密度が増えると、電子がクーロン斥力によって互いに反発するために起きる金属絶縁体転移の「モット転移」によって、「モット絶縁体」が生じることがある。

モット絶縁体は通常「反強磁性」を示し、小さなエネルギーで磁気的な励起(スピン励起)を生じさせることが可能だ。ただし、電気を流すような電荷励起には大きなエネルギーを必要とする。なお、反強磁性とは、電子の上向きスピンと下向きスピンが交互に並んだ磁気秩序が示す磁性のことをいう。

「強相関電子系」(強く相互作用する電子で構成される量子多体系)の根本的問題に関わるものとして、なぜ金属中の電子がスピンと電荷の分離したモット絶縁体になるのかということは長年の謎とされてきたのである。

特に、1986年にベドノルツとミューラーによって「銅酸化物高温超伝導体」が発見されて以降、モット転移に関する理解の重要性が再認識されることとなった。銅酸化物の高温超伝導は、銅と酸素で構成される2次元面のモット転移近傍で現れ、モット転移近傍の性質(特に、モット絶縁体に由来する強い磁気揺らぎ)が、高温超伝導のメカニズムと深く関係していると考えられるようになったことが理由だ。

高温超伝導は金属相とモット絶縁相との間の電子密度の領域で現れ、その領域では金属の自由電子の描像でも、絶縁体の局在電子の描像でも説明し難いさまざまな異常な振る舞いが観測されている。高い温度での超伝導は、こうした異常な振る舞いと関連していると考えられ、その正確な理解が高温超伝導のメカニズム解明に不可欠であると考えられてきた。なお、異常な振る舞いとしては、主に以下の要素が知られている。

• 擬ギャップ(状態密度が減少しているように見えるエネルギー領域)
• フェルミアーク(フェルミ面の一部分が残ったもの。フェルミ面は、無限小のエネルギーで励起された電子の波数を結んだ曲面(2次元系では曲線))
• ドーピング誘起状態(モット絶縁体から電子を取り除くことによってエネルギーギャップ内に生じる励起状態)
• 平坦バンド(エネルギーと波数との関係を表す「分散関係」が平坦な状態)
• (分散関係)キンク(分散関係の折れ曲がり)
• (分散関係)ウォーターフォール(分散関係がほぼ垂直になるとともに、状態密度が極端に減少したように見える振る舞い)
• スピノン的励起状態とホロン的励起状態(スピノンは1次元系で知られているスピンを運ぶ粒子で、ホロンは電荷を運ぶ粒子。反ホロンはホロンの反粒子)
• ホールポケット(モット絶縁体から電子を取り除いた際に生じる空孔が作るフェルミ面)

これまで、これらを断片的なら説明することのできる理論は提案されてきたが、統一的にこれらを説明する理論は確立していなかったのである。

今回の研究によって、高温超伝導体で観測されているさまざまな異常な振る舞いは、金属からモット絶縁体へと移り変わる過程で現れる性質、すなわち、モット絶縁体のスピンと電荷の分離に向けた兆候として、統一的に説明できることが明らかになった(画像1・2)。

モット転移近傍では、「物質中の電子が通常の電子のように振る舞う」(正確には、励起状態(固有状態)が1電子励起によって良く近似できる、という意味)度合いを表す量(1電子励起のスペクトル強度)が幅広いエネルギー・波数領域にわたって濃淡をもって分布する(画像1・2)。そして、その濃淡の変化がモット転移近傍の性質を理解する上で本質的に重要であることがわかった。なお1電子励起とは、最もエネルギーの低い状態の「基底状態」に電子を1つ加える、または取り除く励起のこと。

これに対し、従来の金属の理論(バンド理論)では、物質中の電子は通常の電子のように振る舞うものと見なされるため、分散関係は1つの曲線(曲面)で表され、そのスペクトル強度は電子密度を変えても変化しない。スペクトル強度の濃淡が分布し、それが電子密度に対して変化することは、従来のバンド理論にはない概念であり、それが高温超伝導体の振る舞いが異常と考えられていた要因である。

今回の新概念によって、高温超伝導体のさまざまな異常と思われていた振る舞いは、モット転移近傍の性質の各エネルギー・波数領域における側面として、統一的に理解できることとなった。

今回の研究では、具体的には、2次元系でモット転移を示す最も単純なモデルである「2次元ハバードモデル」に対して「クラスター摂動理論」を適用し、1電子励起のスペクトル強度分布を調べた(画像1・2)。

なお、ハバードモデルとは、格子上を動く電子のいずれか2つが同じ場所に来たときにクーロン斥力によってエネルギーが上昇するとする、電子間相互作用を考慮した金属中の電子に関する最も単純化したモデル。そしてクラスター摂動理論とは、クラスター内の性質を厳密に取り扱い、クラスター間を電子が飛び移る過程では相互作用の影響は小さいものとして近似する数値シミュレーション手法。今回の研究では4×4サイトのクラスターが使用されている。

調査の結果、波数(π,0)付近のω<0の平坦バンドによって擬ギャップやフェルミアークと呼ばれる振る舞いが引き起こされていることがわかった(画像1・2)。また、波数(0,0)-(π,π)方向には1次元系のスピノンとホロンに主に由来する励起状態が現れ、これにより、キンクやウォーターフォールの振る舞いが生じることも判明(画像1・2)。さらに、ω>0の領域にはモット転移に近づくにつれてスペクトル強度を失う状態(ドーピング誘起状態)が現れ、それがモット絶縁体の磁気励起へと連続的に変化することが確認されたのである(画像1～4)。

今回の研究によって、モット転移の本質は、電子のスピン自由度がモット絶縁体の磁気励起に連続的に変化するのに対し、電荷自由度は徐々に凍結することであることが明らかになった。この特徴は、モット絶縁体におけるスピンと電荷の分離に由来しており、スピンと電荷が分離しない「バンド絶縁体」への転移とは本質的に異なる。なおバンド絶縁体とは、電子が占有できる1電子状態(バンド)を電子が完全に占有することによって生じる絶縁体。バンド絶縁体では、スピン励起と電荷励起のエネルギーギャップの大きさは等しい。

そしてこの結論は、以下の研究結果から導かれる。まず画像3に示すように、モット転移近傍での電子の速さ(ω=0での傾き)は、モット絶縁体の磁気励起(スピンの動き)の速さ(点線のω=0での傾き)と同じだ。このことは、電子はモット絶縁体のスピンと同じ速さで動くことを意味する。

しかしながら、ω>0のスペクトル強度は、モット転移に近づくにつれて徐々に失われていく(画像4)。このことは、モット転移に向かって、物質中の電子はスピンと電荷を運ぶ通常の電子のようには振る舞わなくなることを示している。つまり、電子のスピンは連続的にモット絶縁体のものへと変化するのに対し、電荷の自由度は徐々に凍結することを意味しているというわけだ。

このことをより正確に表現すると、以下のようになる。モット転移直前の金属相における1電子励起の分散関係は、2次元系の(0,0)-(π,π)方向では「数式b:画像6」(画像3)、1次元系では「数式c:画像7」と表せる。ここで、v2Dとv1Dは、それぞれ2次元系と1次元系のモット絶縁体における磁気励起の速さである。なお、2次元系の場合に√2がついているのは、(0,0)-(π,π)方向の分散関係であるためだ。

これらの分散関係を用いて、モット絶縁体の磁気励起の分散関係は、2次元系の(0,0)-(π,π)方向では「数式d:画像8」、1次元系では「数式e:画像9」と表される。このことから、金属相の1電子励起の分散関係はモット絶縁体の磁気励起の分散関係と直接関係していることがわかるというわけだ。

また、モット転移に近づくにつれて、電子を加える1電子励起(ω>0)は徐々にスペクトル強度を失い、モット転移点では0になる(画像4)。このことは、モット転移に向けて、電子のスピン自由度が連続的にモット絶縁体の磁気励起へと変化するのに対し、電荷自由度は徐々に凍結することを意味する。このモット転移の特徴は、1次元系では厳密解を用いて示されており、今回、2次元系でも同様な特徴が現れることが明らかになった。

これまで、いくつも提案されてきた高温超伝導に関する理論。その妥当性は、高温超伝導体で観測されているさまざまな異常な振る舞いをどれだけ統一的に説明することができるかによって判断される。特に、モット絶縁相と異常な金属相(および超伝導相)との関連が大きな争点となっていた。

そして今回の研究によって、異常な振る舞いのほとんどが2次元ハバードモデルによって説明できることと、異常な金属相とモット絶縁相との関連が明らかになったのである。これにより、高温超伝導のメカニズム解明への道筋が開けたといえよう。

環境エネルギー問題の解決のため、より高い転移温度をもつ高温超伝導体の探索が続けられている。高温超伝導のメカニズムに関する理解が深まれば、高温超伝導体の探索指針を示すことができ、より効率的な探索が可能になると考えられる次第だ。

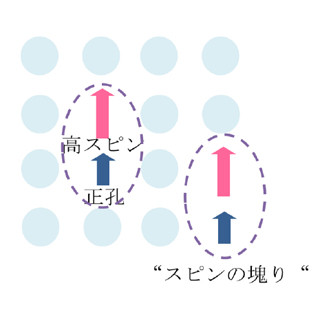
モット転移に関する理解は、新しい高温超伝導体の探索ばかりではなく、次世代の強相関スピントロニクスへの応用も期待される。今回の研究によって、モット転移近傍(画像10)では、モット絶縁体のスピンと電荷の分離を反映した特異な性質が現れることが明らかになった。この特異な性質をスピントロニクスに応用することができれば、スピンと電荷の性質を利用した新しい動作原理に基づくデバイスが得られる可能性があると、研究グループでは語っている。

なお、今回の研究では、モット転移近傍の異常な振る舞いと超伝導とを直接関係づける証拠は得られなかったが、高温超伝導体の研究において最も問題となっていたさまざまな異常な振る舞いを統一的に説明することができた。これにより、高温超伝導のメカニズム解明向けて今後の飛躍的進展が期待されると、研究グループではコメントしている。