近似曲線を利用するときの注意点

Excelにはグラフに近似曲線を追加できる機能が用意されている。ただし、この機能を安直に使ってしまうと、データを分析する際に大きなミスを犯してしまう恐れがある。今回は、近似曲線を利用するときの注意点について簡単に説明しておこう。

近似曲線をグラフに追加する手順

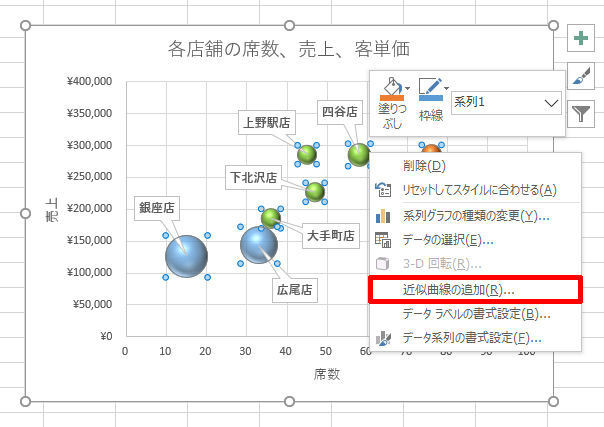
まずは、グラフに近似曲線を追加するときの操作手順を“おさらい”しておこう。近似曲線を追加するときは、データ部分（バブルや棒グラフなど）を右クリックし、「近似曲線の追加」を選択すればよい。

• 近似曲線の追加

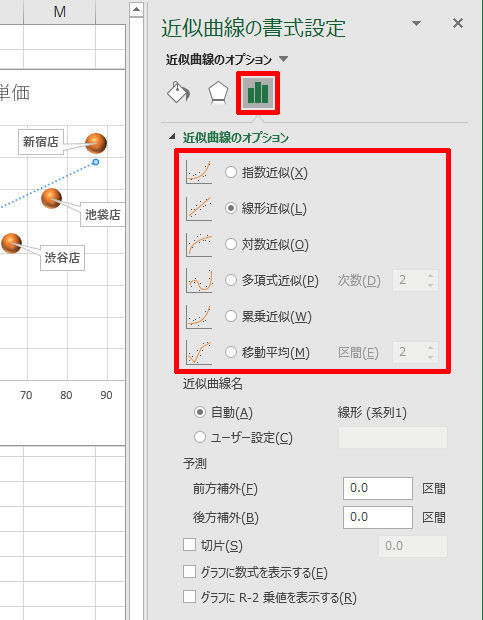
すると、「近似曲線の書式設定」が表示される。ここでは、最初に「近似方法」を選択する。X軸とY軸のデータが比例関係にあると考えられる場合は「線形近似」を選択するのが基本である。

今回の例の場合、「席数」に比例して「売上」も伸びるはず、と考えられるので「線形近似」のままで構わない。

• 近似方法の選択

なお、X軸とY軸が指数的もしくは対数的に変化すると考えられる場合は、「指数近似」や「対数近似」を選択しなければならない。そのほか、「多項式近似」や「累乗近似」といった近似方法も用意されているが、その意味がよくわからない場合は、これらの項目を選択しないのが基本である。「なんとなく正しい曲線になりそうだから・・・」という安直な考えで選択すると、何の根拠もない近似曲線が描画されてしまうことに注意しよう。

なお、最後にある「移動平均」の選択肢は、本連載の第5回で紹介した移動平均と同じ処理を行うものである。この機能を使うと、自分で計算を行わなくても、グラフに移動平均線を描画することができる。

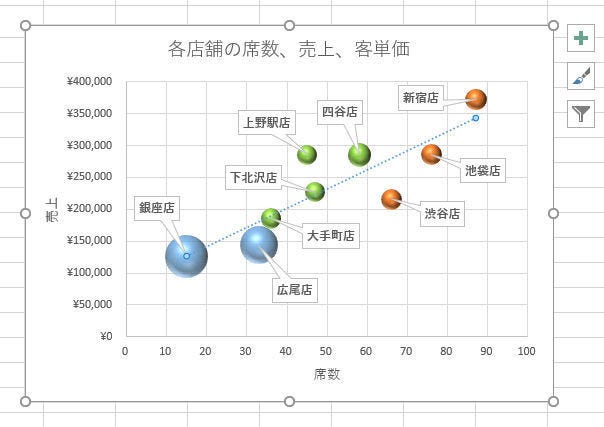
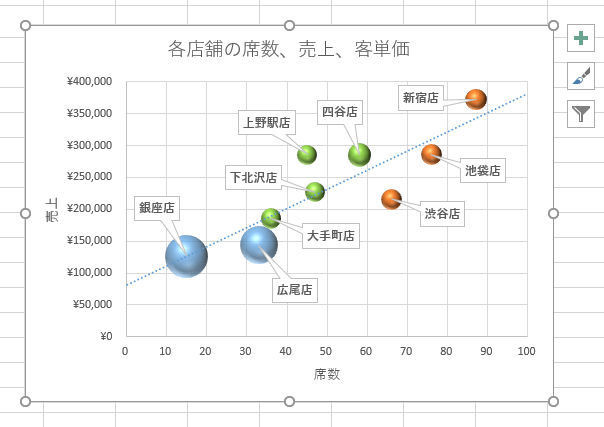
話を「各店舗の席数、売上、客単価」に戻して解説を進めていこう。近似方法に「線形近似」を選択すると、以下の図のような直線が表示される。

• 近似曲線が追加されたグラフ

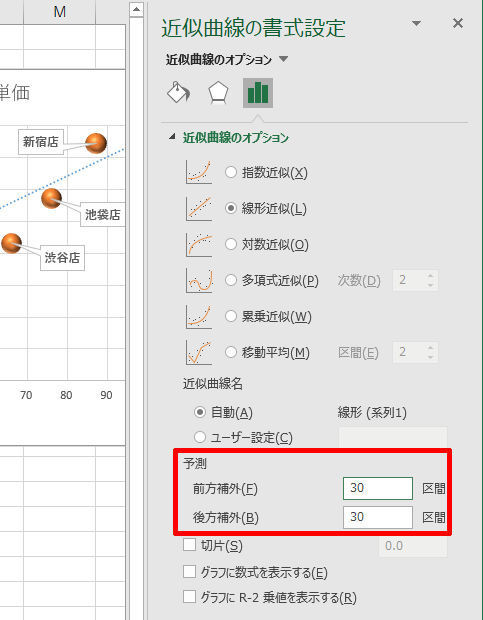
この近似曲線（直線）は、データがある範囲だけに表示されるように初期設定されている。これをグラフの端から端まで伸ばすには、「前方補外」と「後方補外」に適切な数値を指定しなければならない。

これらの項目には「X軸方向にどれだけ伸ばすか？」を指定するのが基本であるが、いちいち計算するのが面倒な場合は、（少し大きめの）おおよその数値を指定しても構わない。この場合、近似曲線（直線）がグラフの外に飛び出すことになるが、実際には描画されないので特に問題は生じないだろう。

• 「前方補外」と「後方補外」の指定

• 伸長された近似曲線

もちろん、近似曲線（直線）の書式を変更することも可能である。この場合は、近似曲線を右クリックし、「枠線」から書式を指定すればよい。

• 近似曲線の書式指定

以上が、近似曲線をグラフに追加するときの基本操作となる。

その近似曲線は本当に適切か？

前述したように、Excelを使うと、難しい計算を行わなくても、手軽に近似曲線を描画することが可能となる。この近似曲線（直線）は、評価の基準線などに活用できる。

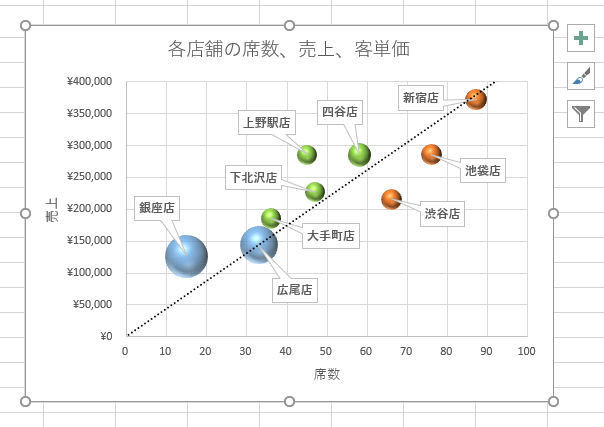
ここからは「前回の連載の続き」について話を進めていこう。前回の連載では、バブルチャートに近似曲線を追加して以下のようなグラフを作成した。

• 前回の連載で作成したグラフ

このグラフに従うと、店の規模（席数）に対して大きな売上を記録しているのは「上野駅店」であることが分かる。「新宿店」と「四谷店」も健闘している、と評価できるだろう。一方、「池袋店」、「渋谷店」、「広尾店」の3店舗は、規模のわりに売上が小さい、という評価になる。

しかし、これは本当であろうか？　グラフに描画された近似曲線（直線）をよく見ると、少し不可解な点があることに気付く。それは「席数」が0のときに約8万円の「売上」になる、と示されていることだ。

一般的に考えて「席数」が0の店舗というのはあり得ないが、仮に存在するとすると、その「売上」は0円になると考えられる。しかし、近似曲線（直線）では約8万円の売上と示されている。

このように考えれば、この近似曲線は「適切ではない」という結論に至るはずだ。正しい近似曲線は、原点（0,0）を通るべきである。

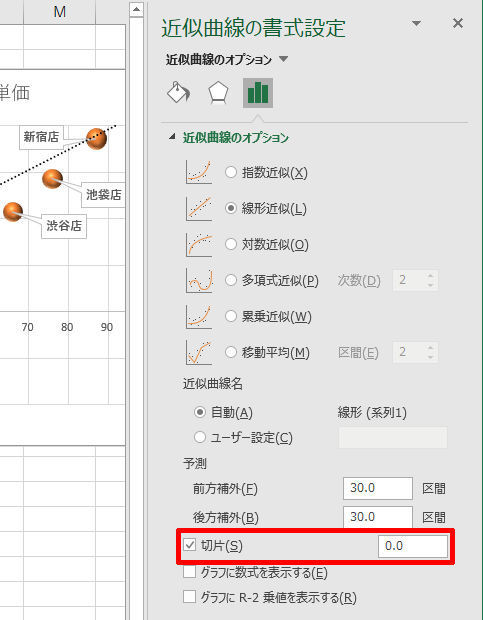
このような場合は、近似曲線をダブルクリックして設定画面を開き、「切片」の項目を指定しなければならない。「切片」は「Y軸とどこで交わるか？」を指定するもので、ここに0を指定すると必ず原点（0,0）を通る近似曲線を描画できる。

• 切片の指定

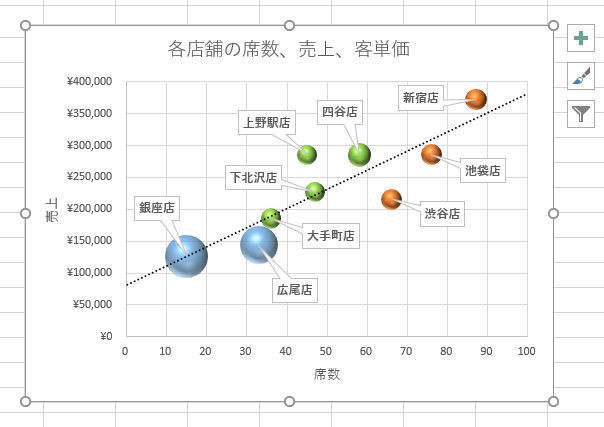
設定を変更すると、近似曲線の表示は以下の図のように変化する。

• 切片を0にした近似曲線

このグラフを見ると、店の規模（席数）に対して大きな売上を記録しているのは、「上野駅店」、「四谷店」、「下北沢店」、「大手町店」、「銀座店」の5店舗であることが分かる。前回の例とは少し違う結果だ。

また、前回のグラフで「健闘している」と評価された「新宿店」は、どちらかというと近似曲線より下に位置することになり、「規模のわりに売上が小さい」という真逆の評価になってしまう。

このように近似曲線を「評価の基準」にするときは、近似曲線が「状況を正しく再現しているか？」をよく検討しなければならない。これが間違っていると、当然ながら、間違った評価・分析をしてしまうことになる。よって、十分に注意しなければならない。

近似曲線と平均値について

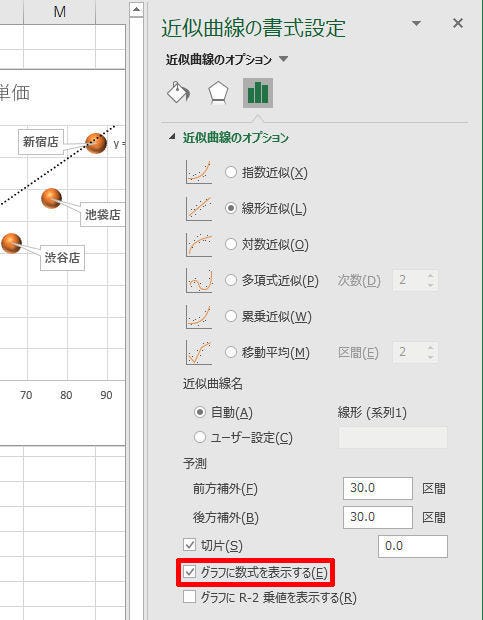
もう少し補足しておこう。「近似曲線の書式設定」には「グラフに数式を表示する」という項目も用意されている。このチェックをONにすると、近似曲線の「数式」をグラフ内に示すことができる。

• 数式の表示設定

• 近似曲線の数式を表示したグラフ

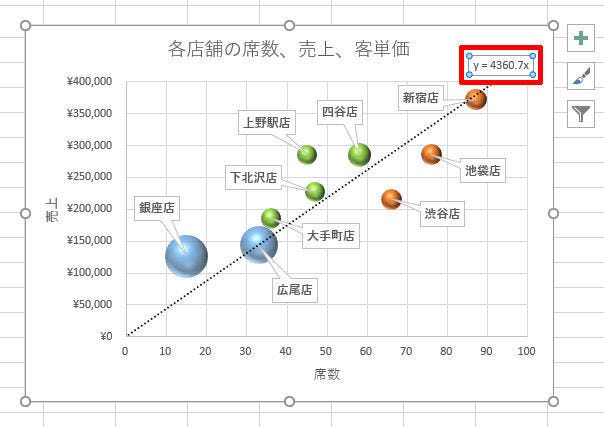
この数式をデータ分析に活用することも可能だ。今回の例では「y=4360.7x」という数式が表示されているので、「1席あたり4360.7円の売上」が評価の基準になっている、と考えられる。

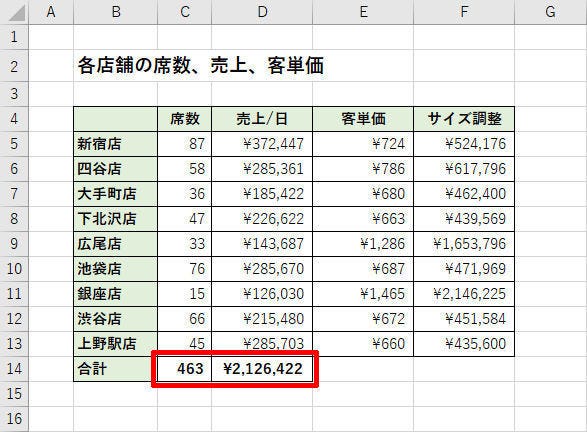
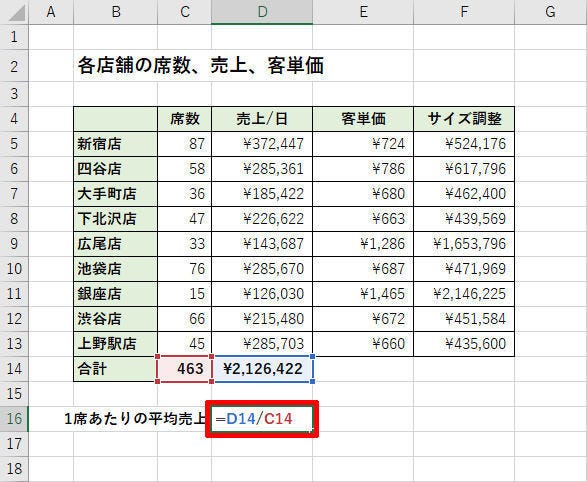
では、実際のデータについてはどうであろうか？　続いては「1席あたり平均売上」を計算してみよう。まずは、全店舗について「席数」と「売上」の合計を関数SUM()で算出する。

• 「席数」と「売上」の合計を算出

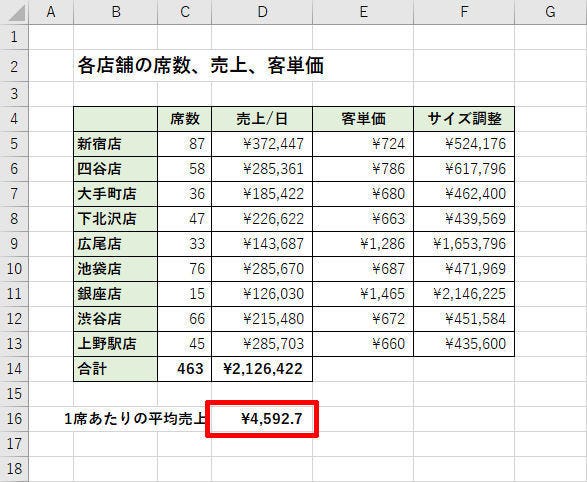
続いて、この合計について「売上」÷「席数」を計算すると、「1席あたりの平均売上」」を求めることができる。

• 「1席あたり平均売上」を算出する数式

• 「1席あたり平均売上」の計算結果

この結果は約4,592.7円となり、先ほど示した「近似曲線の数式」とは少し異なる値になる。それもそのはず。両者は全く別の計算手法により算出された値となるからだ。

近似曲線（線形近似）では、最小二乗法と呼ばれる手法により「傾き」（1席あたりの売上）が計算される。ちなみに、最小二乗法は「近似線」と「実データ」の差の2乗が最小になるように直線を求める計算手法となる。

一方、先ほど自分の手で計算した「1席あたり平均売上」は、あくまで全店舗の平均を求めたものにすぎない。よって、その計算結果は異なる値になる。

このように、近似曲線について突き詰めていくと、とても奥の深い、ややこしい話になってしまう。正しく理解するには統計学の書籍をよく読み、理解することが求められるが、それは少しハードルの高い話である。

そもそも、「席数に比例して売上も増加するはず」という理論そのものが間違っている可能性もある。統計学にもとづいた分析はそれなりに効果のあるものであるが、一つ間違えると無意味で信頼性に欠ける結論が導き出されてしまう恐れがある。ただでさえ机上の空論になりがちなので、近似曲線を利用するときは十分に注意しなければならない。「何となく正しそう・・・」と安直に利用するのは非常に危険である。