第13回では、「進めるだけ進み、行き詰まったら1歩戻る」という方針でグラフを探索する「深さ優先探索」を取り上げましたが、グラフに関するアルゴリズムはこれだけではありません。今回は最短経路を求めるときにも使える「幅優先探索」を紹介します。
第13回「身近な『掃除』を例に考える、『深さ優先探索』とは?」はこちらから
幅優先探索とは
幅優先探索は、スタートに近い頂点から順番にグラフを探索していくアルゴリズムです。英語で「 Breadth First Search 」と書くため、略して BFS と呼ばれることもあります。
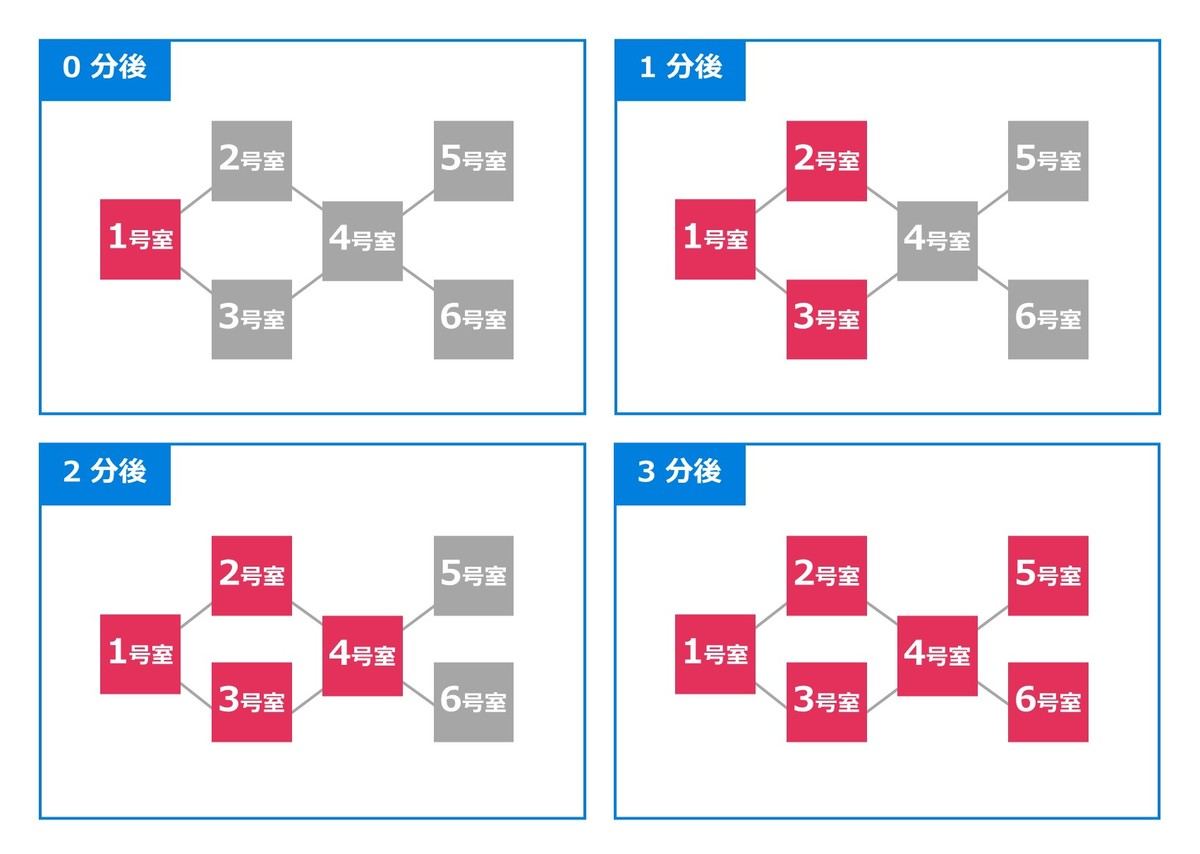
幅優先探索のイメージを理解するために、冷房の問題を考えてみましょう。具体的には、部屋 1 の冷房のスイッチを入れ、部屋 1 が涼しくなったという状況を考えます。1 分で「隣接する部屋」が涼しくなるとき、各部屋は何分後に涼しくなるのでしょうか。
答えは部屋 1 から順に 0 分・1 分・1 分・2 分・3 分・3 分です。冷房の場所(部屋 1)から考えていくと、下図のようにして答えを求めることができます。冷房の効き具合を 1 分ごとにシミュレーションしていると捉えることもできますね。
最短経路長とは
次のステップに進む前に、重要な用語を整理しましょう。グラフ上の 2 点間を結ぶ経路(パス)のうち最も短いものを「最短経路」と言います。具体的には、下記のとおりです。
| 重みなしグラフの場合 | 重み付きグラフの場合 |
|---|---|
| 通る辺の数が最小となる経路 | 通る辺の重みの合計が最小となる経路 |
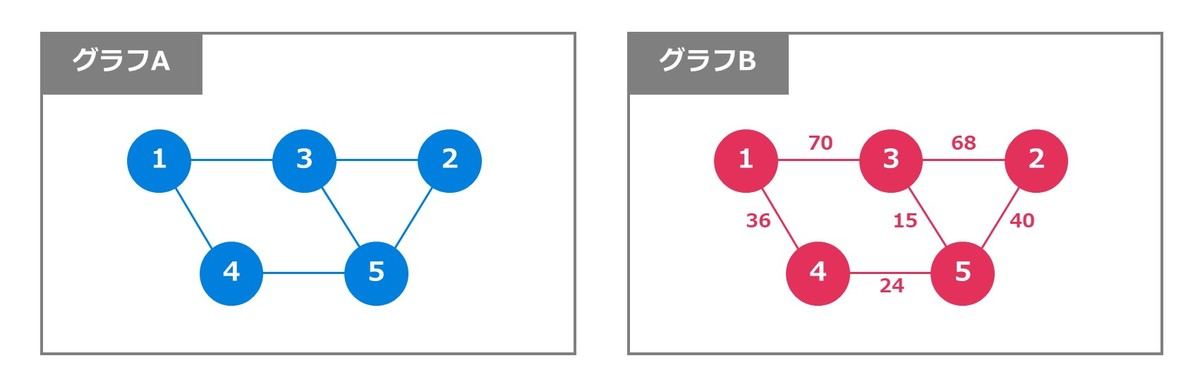
下図の重みなしグラフ A における頂点 1 から 2 までの最短経路は 1→3→2 であり、通る辺の数は 2 です。また重み付きグラフ B における頂点 1 から 2 までの最短経路は 1→4→5→2 であり、通る辺の重みの合計は 100 です。
最短経路長の求め方 (1):直感的な方法
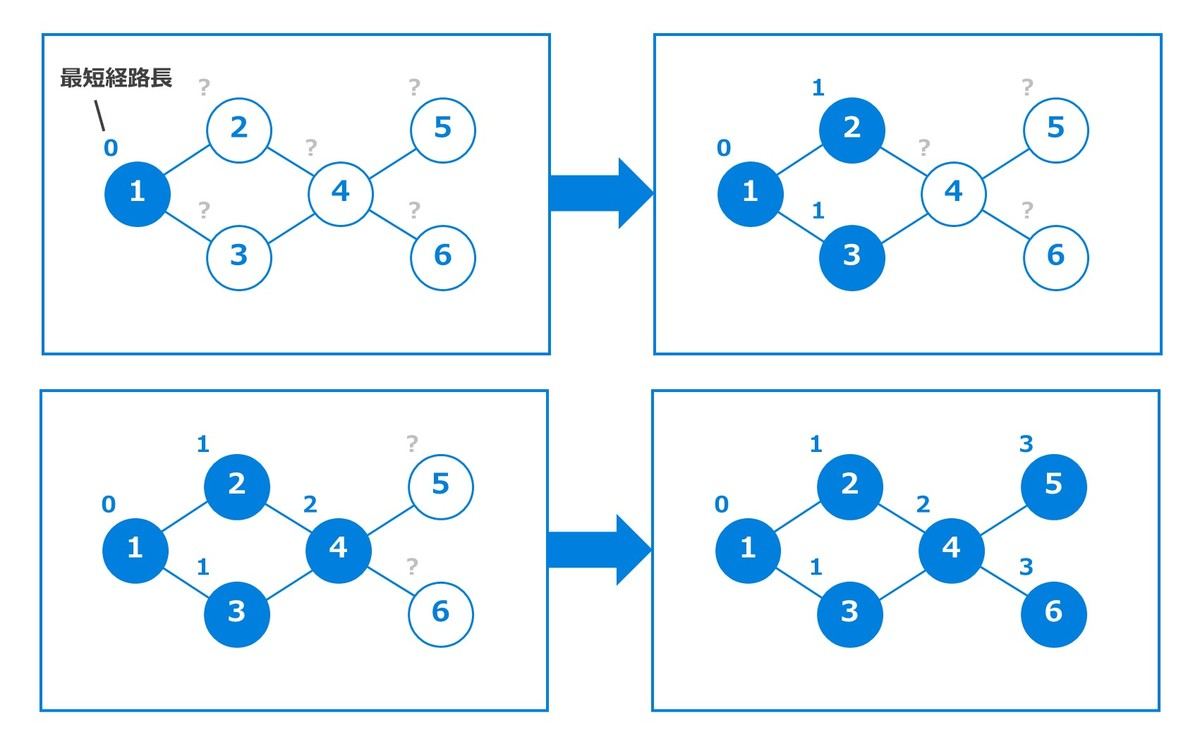
それでは、今回のメインとも言える最短経路問題に入ります。重みなしグラフについて、頂点 1 から各頂点までの最短経路長はどうやって計算できるのでしょうか。結論としては、次のような非常に単純なアルゴリズムが通用します。
- スタート地点である頂点 1 に「0」と書き込む
- 「0」の隣(頂点1に隣接する頂点)に「1」を書き込む
- 「1」の隣に「2」を書き込む。
- 「2」の隣に「3」を書き込む。(以下略)
なぜなら、前述した冷房問題における「涼しくなるまでの時間」と最短経路長は一致するからです。以下に例を示します。
最短経路長の求め方 (2):キューを使った方法
確かに前述のアルゴリズムでも、最短経路長を正しく求めることができます。しかし何の工夫も行わなければ、頂点数を N 、最短経路長の最大値を D とするとき、計算量 O(ND) を要します※1。
そこで一般的な幅優先探索ではキュー※2を使います。少し複雑ですが、頂点 x までの最短経路長を dist[x] とするとき、アルゴリズムの流れは以下の通りです。
手順1 頂点 1 以外を白色で塗り、
dist[x]=?に初期化する。
手順2 頂点 1 を青色で塗り、dist[1]=0にする。キューに頂点 1 を追加する。
手順3 キューが空になるまで、以下の操作を繰り返す。
- キューの先頭要素
posを調べる。- キューの先頭要素を削除する。
- 頂点
posに隣接する白色頂点nexに対して、dist[nex]をdist[pos]+1に更新し、キューに頂点nexを追加する。頂点nexは青色で塗る。
このアルゴリズムを具体的なグラフに適用させると下図のようになります。この図では、頂点 pos を赤色の三角形で示しています。
※1 整数 a の隣に a+1 を書く操作を行うためには、「どの頂点が整数 a であるのか」を調べる必要があります。この処理に計算量 O(N) がかかりますが、実際はこれを D 回繰り返すため、計算量は O(ND) です。 ※2 キューについては、本連載の第11回を参照してください。
幅優先探索の正当性
幅優先探索の動きは少し複雑ですが、必ず以下の順序でキューに追加されていきます。
- 最初に、最短経路長 0 の頂点が追加される
-
dist[pos]=0のとき、最短経路長 1 の頂点がキューに追加される -
dist[pos]=1のとき、最短経路長 2 の頂点がキューに追加される -
dist[pos]=2以降も同様
このことが、最短経路長を正しく求められる理由になっています。
幅優先探索の実装
最後に、幅優先探索のアルゴリズムを Python で実装すると以下のようになります。キューを管理できる deque モジュールが分からない方は、本連載の第 11 回に戻って確認しましょう。なお、頂点数を N、辺数を M とするとき、プログラム全体の計算量は O(N+M) です。
from collections import deque
# グラフの例(図に対応)
N = 6
M = 6
A = [1, 1, 2, 3, 4, 4]
B = [2, 3, 4, 4, 5, 6]
# 隣接リストの作成
G = [ list() for i in range(N + 1) ]
for i in range(M):
G[A[i]].append(B[i])
G[B[i]].append(A[i])
# 幅優先探索の初期化 (dist[x]=? の代わりに dist[x]=-1 に初期化していることに注意)
dist = [ -1 ] * (N + 1)
Q = deque()
dist[1] = 0
Q.append(1) # Q に 1 を追加
# 幅優先探索
while len(Q) > 0:
pos = Q.popleft() # Q の先頭を調べ、これを取り出す
for nex in G[pos]:
if dist[nex] == -1:
dist[nex] = dist[pos] + 1
Q.append(nex) # Q に nex を追加
# 頂点 1 から各頂点までの最短距離を出力
for i in range(1, N + 1):
print(dist[i])
第11回「代表的なデータ構造 -『スタック』『キュー』『優先度付きキュー』とは?」はこちらから
* * *
今回は「冷房の効きの広がり」を例に、幅優先探索を紹介しました。幅優先探索を利用すると、重みなしグラフの最短経路長を求めることができます。次回は重み付きグラフの最短経路を求めるのに便利な「ダイクストラ法」をご紹介します。楽しみにお待ちください。