前回の記事では、重みなしグラフの最短経路問題を解くアルゴリズムである「幅優先探索」を説明しました。
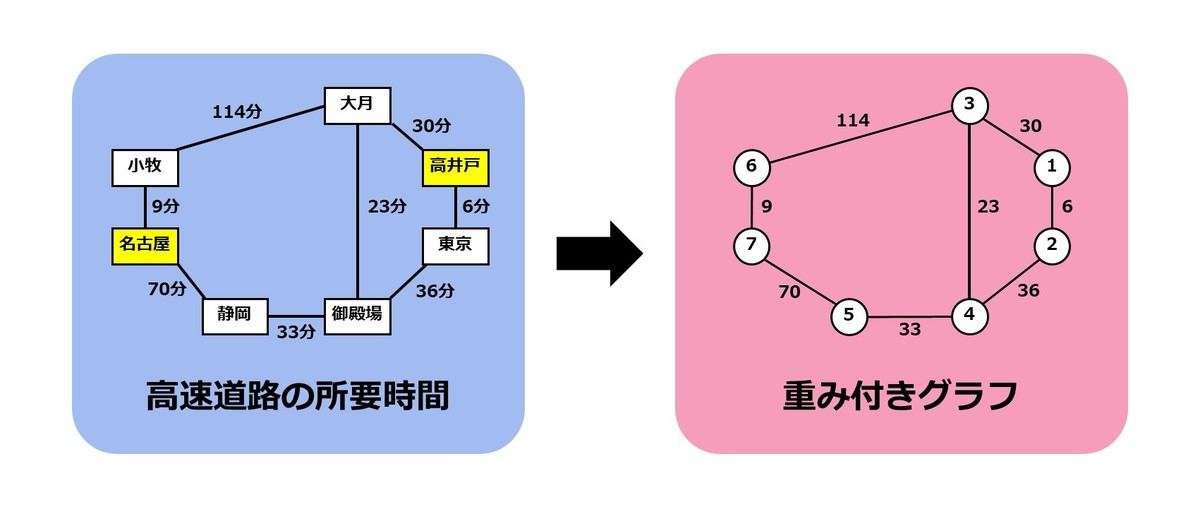
しかし、高速道路の所要時間(下図)など、現実の問題設定の多くは重み付きグラフで表されます。そのため、例えば「高井戸 IC から名古屋 IC までの最短時間は何分か?」という問題に答えたい場合、重み付きグラフの最短経路問題を解く必要があるのです。
では、重み付きグラフの最短経路問題はどうやって解けば良いのでしょうか。今回の記事では、一つの解決策として「ダイクストラ法」を紹介します。
ダイクストラ法とは
ダイクストラ法は、以下の 2 つのルールにしたがって、最短経路長を求めるアルゴリズムです。
ルール1 スタートに近い頂点から順番に、答えを確定させていく
ルール2 答えが確定したら、その頂点に隣接する頂点の最短経路長を更新する
例として、上図の高速道路における、高井戸 IC から各地点までの最短時間を求めることを考えましょう。
ステップ1
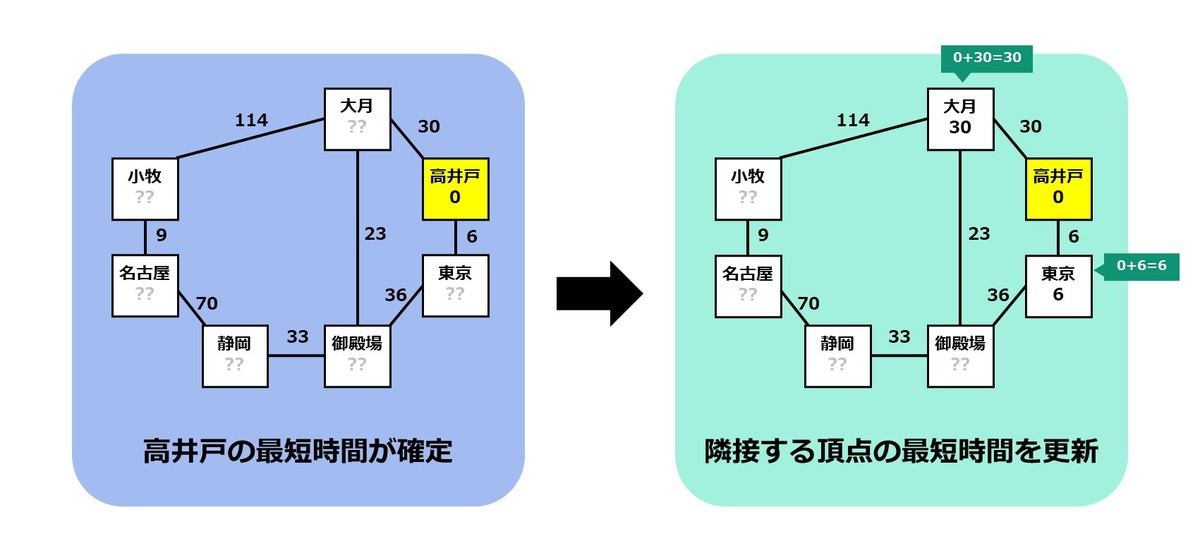
まず、スタートに最も近い頂点は「高井戸」ですので、高井戸までの最短時間を 0 分で確定させます。また、高井戸から東京までは 6 分、高井戸から大月までは 30 分で移動できるので、以下の更新を行います。
- 東京までの最短時間: 0+6=6 分
- 大月までの最短時間:0+30=30 分
ここまでの流れをまとめると、下図のようになります。(最短時間が確定した頂点を黄色で表しています)
ステップ2
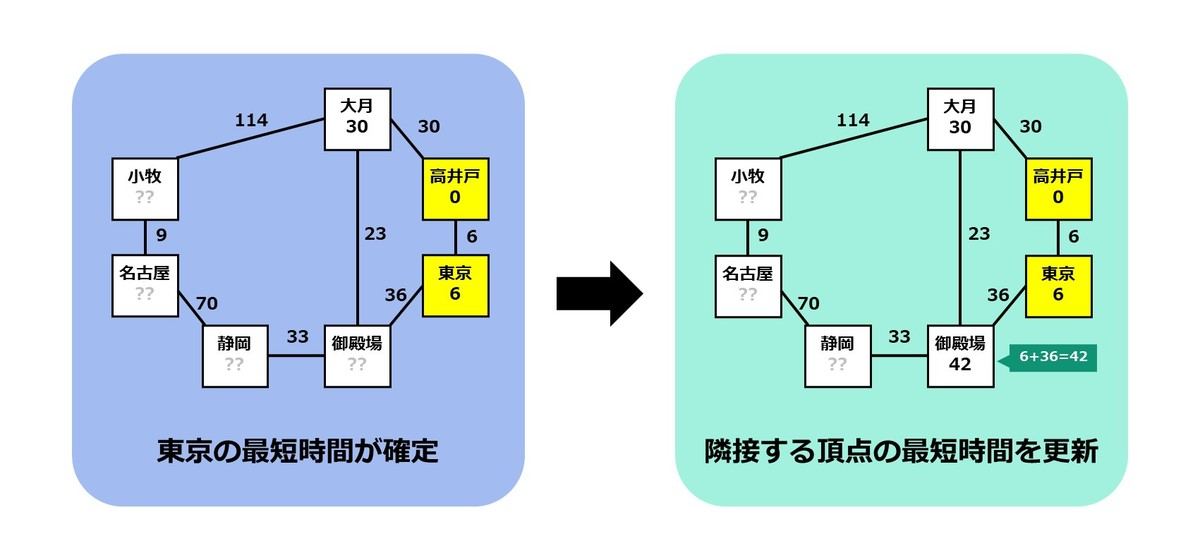
それでは、次に近い頂点はどこでしょうか。現時点では、東京が 6 分、大月が 30 分と書かれているので、答えは「東京」です。そこで、東京までの最短時間を 6 分で確定させます。また、東京から御殿場までは 36 分で移動できるので、以下の更新を行います。
- 御殿場までの最短時間: 6+36=42 分
なお、東京からは高井戸に行くこともできますが、高井戸の最短時間はすでに確定しているため、更新を行わないことにします。
ステップ3
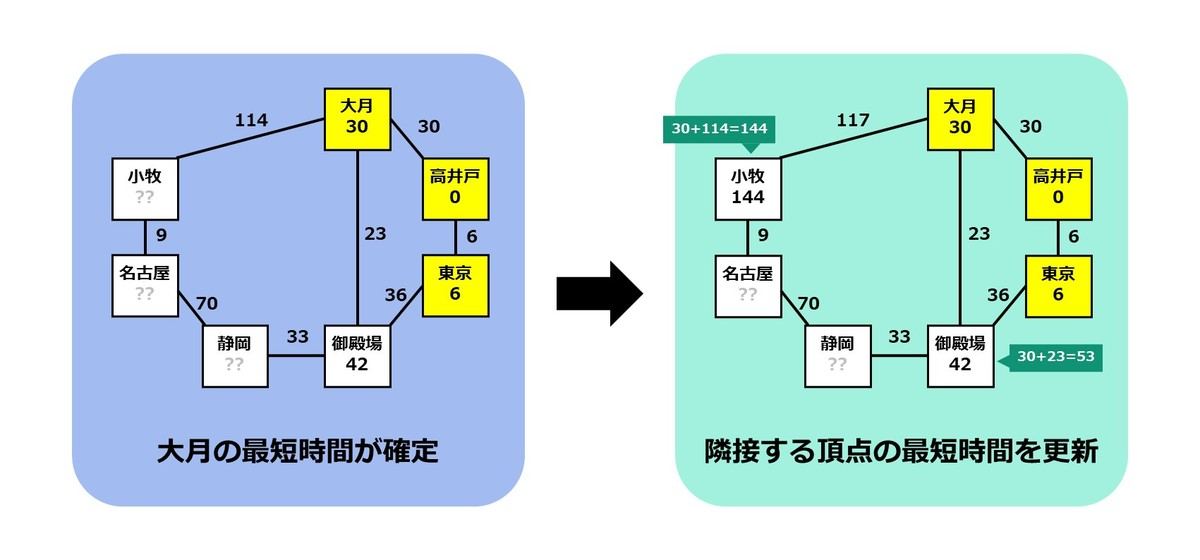
次に近い頂点は「大月」ですので、大月までの最短時間を 30 分で確定させます。また、大月から小牧までは 114 分で移動できるので、以下の更新を行います。
- 小牧までの最短時間: 30+114=144 分
なお、大月からは御殿場にも行くことができますが、このルートでは 30+23=53 分かかり、現時点での値「42 分」に負けてしまうため、更新を行わないことにします。
ステップ4
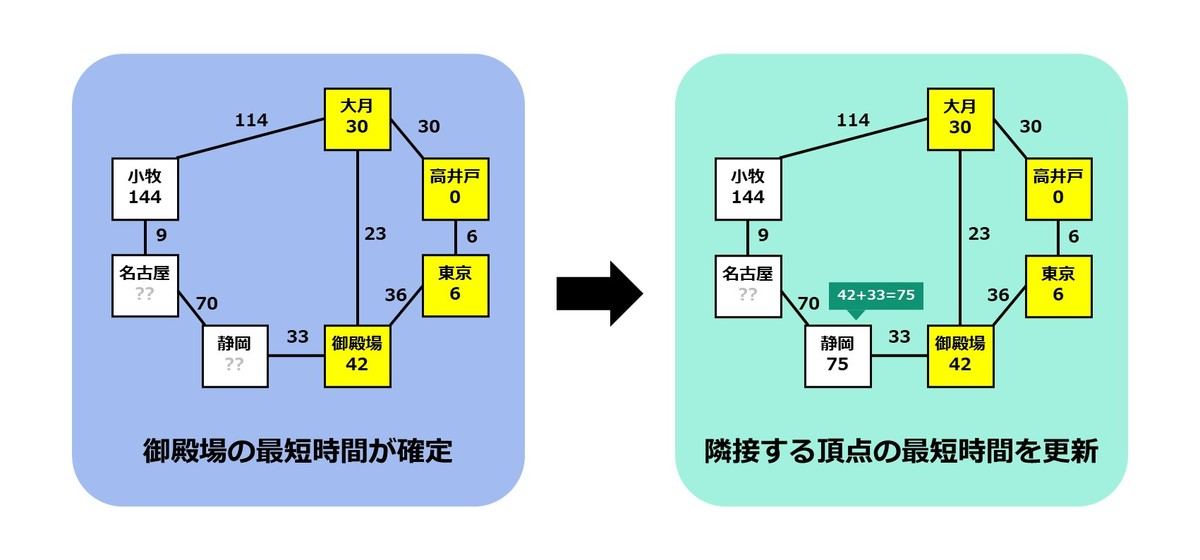
次に近い頂点は「御殿場」ですので、御殿場までの最短時間を 42 分で確定させます。また、御殿場から静岡までは 33 分で移動できるので、以下の更新を行います。
- 静岡までの最短時間: 42+33=75 分
ステップ5
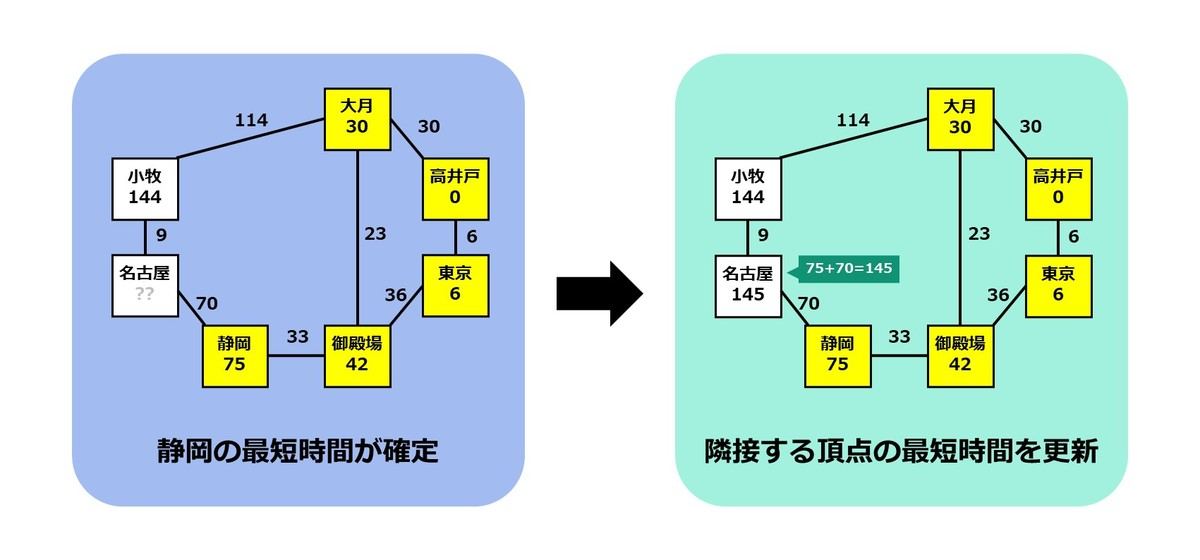
次に近い頂点は「静岡」ですので、静岡までの最短時間を 75 分で確定させます。また、静岡から名古屋までは 70 分で移動できるので、以下の更新を行います。
- 名古屋までの最短時間: 75+70=145 分
ステップ6
次に近い頂点は「小牧」ですので、小牧までの最短時間を 144 分で確定させます。ここで、小牧からは名古屋へ 9 分で移動することができますが、このルートでは 144+9=153 分かかってしまいます。これは、現時点での値「145 分」に負けるため、最短時間を更新しないことにします。
ステップ7
最後に、残っている頂点「名古屋」までの最短時間を、145 分で確定させます。これで、高井戸から各地点までの最短経路長が、以下の表のとおりであることが判明しました。ダイクストラ法の流れについては、理解できましたか。
| 高井戸 | 東京 | 大月 | 御殿場 | 静岡 | 小牧 | 名古屋 |
|---|---|---|---|---|---|---|
| 0 分 | 6 分 | 30 分 | 42 分 | 75 分 | 144 分 | 145 分 |