京都大学(京大)は7月4日、量子力学が支配するミクロな世界では時間が逆戻りできる可能性がある“可逆的なシステム”であるにもかかわらず、なぜ我々の住むマクロな世界になると、時間が過去から未来へと一方的にしか流れない「時間の矢」が生じるのか、その理由を解明する具体的な物理モデルの構成に成功したと発表した。
同成果は、京大 情報学研究科の大久保健一大学院生(現・公立諏訪東京理科大学 講師)、同・梅野健教授の研究チームによるもの。詳細は、米国物理学協会が刊行する非線形ダイナミクスと複雑系を扱う学術誌「Chaos:An Interdisciplinary Journal of Nonlinear Science」に掲載された。
「時間の矢の問題」は、量子力学が支配するミクロな世界が持つ時間的な「可逆性」と、我々が認識するマクロな世界における時間的な「不可逆性」の間に存在する矛盾を指す。ミクロな世界での現象は時間的に前後どちらにも起こりうるように見えるが、マクロな世界では過去から未来への一方的な時間の流れしか観測されない。この根本的な理由は、物理学における大きな未解決問題である。
時間の矢の問題に関する研究は、19世紀後半にオーストリアの物理学者ルートヴィッヒ・ボルツマンが提唱した、熱力学第二法則における「エントロピー増大則」に端を発する。その後、20世紀半ば以降になり、さまざまな物理系で“カオス”現象が発見されたことで、時間の矢に関する研究は大きく進展することになる。
カオスとは、ごくわずかな初期状態の違いが、後の結果に大きな差をもたらす現象のことで、天気予報の長期予測が困難なのもこのカオス性が一因とされる。しかし、一見予測不可能なカオス的な動きの中にも、初期の情報が時間経過と共に失われ、最終的に均一な状態へ落ち着く性質である「混合性」があることが判明している。
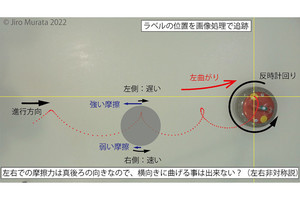
そんな混合性は不可逆性と密接な関係にあり、マクロな世界で時間が一方向に流れる理由を説明する手がかりとして期待された。しかし、時間的に逆転可能な物理法則に従う系でこの混合性が具体的に示された例は、ビリヤード系や負曲率多様体上の測地線運動など、ごく一部に限られていたのが実情だ。
そうした中で20世紀末に誕生したのが、「可解カオス」の概念だ。これは、三角関数の1つである正接(タンジェント)関数の加法公式から導かれる、混合性を持ち、平衡状態が安定分布である「コーシー分布」に収束する系のこと。研究チームがそれを受けて明らかにしたのが、この可解カオスが周期ポテンシャル「log(|cosx|)」によって構成され、運動量方向で「超拡散」が生じるという点だった。
2017年ごろに研究チームは、同じポテンシャル系に2次の「対称型シンプレクティック積分法(リープフロッグ法)」を適用し、任意の時間Δτで差分化しても、元の微分方程式系が持つ「時間反転対称性」を保存する物理系の構成に成功していた。なお時間反転対称性とは、物理システムの運動を記述する方程式が、時間の進む方向を過去へと向けても不変である性質のこと。そこで研究チームは今回、この成果のさらなる発展を目指したという。
今回の研究では、上述した系において強い混合性を示す特性である「アナソフ性」の証明に成功した。これにより、系がただ1つの平衡状態に収束するという不可逆性を持つことが示され、その平衡状態が物理的な測度である「SRB(シナイ=リュエール=ボウエン)測度」であることも判明した。さらに、力学的なエントロピー生成率を指す「コルモゴルフシナイエントロピー」が正であること、同エントロピーと正の「リアプノフ指数」に等しいという「ペシンの等式」など、多岐にわたる性質が証明された。
今回証明されたように、一般的には古典力学(ニュートン力学)の支配するマクロな世界においては混合性の概念が存在し、不可逆性の証明が可能だ。しかし、ミクロな世界を支配する量子力学は、古典力学と同様に時間反転対称性を持つものの、混合性の概念そのものが存在しない。そのため、今回の手法で時間の矢を示すのは困難であり、新たな概念が必要となる。不可逆性を示す混合性やアナソフ性といった古典力学の中で生まれた概念が、量子力学といかに両立するのかは、今後も引き続き難問として残るとした。
また研究チームによると、今回の成果は応用面でも重要性を持つといい、特に、機械学習アルゴリズムの「ハミルトンモンテカルロ法」で用いられる2次のシンプレクティック数値積分法が、アナソフ性の鍵となった点は大きいという。この発見は、平衡状態へ効率よくサンプリングさせるカオス的なサンプリング法、つまり「シンプレクティックなカオスモンテカルロ法」の構築につながる可能性を秘め、今後の研究進展が期待されるとしている。