日本科学未来館でメディアラボ第11期「フカシギの数え方」がスタート

日本科学未来館では、おおよそ半年ごとに3階の常設展示の1つ「メディアラボ」の展示内容を一新している。この8月1日からは、第11期展示となる「フカシギの数え方 The Art of 10の64乗 -Understanding Vastness-」がスタートした(画像1・2)。2013年2月25日(月)まで開催。内覧会に参加してきたので、その模様をリポートする。

これまで、メディアラボは「デバイスアート」と呼ばれる、日本発の電子機器を用いた新しいアートの潮流を、その創作活動を行っているクリエイター及びクリエイティブ性の高い研究者たちの個展というスタイルで、それまでに作られてきた作品の数々を展示してきた。

しかし、今回からは若干趣向が変わり、日本の最先端の研究内容を子どもたちも含めた一般の方々に楽しんでもらえるような形で紹介するというスタイルとなったのである(実際には、第9期「もんもとすむいえ」もこれに近い形だった)。

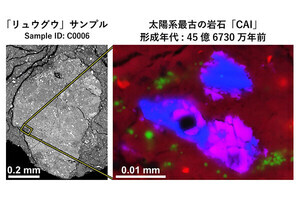
今回は、「JST(科学技術振興機構)ERATO(エラト)湊離散構造処理系プロジェクト」が題材。北海道大学 大学院情報科 科学研究科 コンピュータサイエンス専攻教授で、同プロジェクトの研究総括を努める湊真一博士の研究内容を扱っている。タイトルからも想像がつくように、数に関係する面白さと、研究内容が紹介されているのだ(画像3)。

ちなみに、タイトルにある「フカシギ」というのは、日本の21単位ある(22単位とする説もある)数の単位(数詞)の20単位目、10の64乗から67乗(10の後ろに0が64～67個つく)までを表す「不可思議」のことだ。そして、タイトルの最後の英単語「Vastness」とは、広大という意味である。不可思議という単位まで行くと、広大無辺さを感じるわけで、それを実感できるのが、今回の展示でもあるのだ。

では、その不可思議がどれぐらいの大きさの数字なのかを実感してもらおう。まずは、65桁の数字を羅列してみる。「12,345,678,912,345,678,912,345,678,912,345,678,912,345,678,912,345,678,912,345,678,912」という具合だ(数字の意味はない)。

この欧米式に3桁ごとにカンマで区切っても、もはや見やすいとかわかりやすいとかそういうレベルを超えており、ただただ数字がいくつも並んでいるとしか思えない。そこで、もう少しわかりやすくするため、日本ならではの漢字の単位を4桁ごとに入れて見る。

すると、「1不可思議2345那由他6789阿僧祇1234恒河沙5678極9123載4567正8912澗3456溝7891穣2345じょ(画像4)6789垓1234京5678兆9123億4567万8912」という具合だ。なお、上の方の単位の読み方は、那由他=なゆた、阿僧祇=あそうぎ、恒河沙=ごうがしゃ、極=ごく、載=さい、正=せい、澗=かん、溝=こう、穣=じょう、垓=がい、である。

この中で、知られている単位といえば、せいぜいスパコン「京」や「宇宙鉄人キョーダイン」(笑)で知られた京が上限だろう。その先は読み方だけでなく、単位そのものを知らない、聞いたことはあっても実際に何かを数えるのに使ったことはない、という人が普通ではないだろうか。

となると、こんな膨大な数字、我々の日常の生活に何の関係があるの? と多くの人が疑問に持つことだろう。なぜわざわざ予算を使ってまで研究しているのか、といぶかしむ人もいるかも知れない。

しかし、こんな天文学的な数字だが、意外と日常的なものの中でそれに近い数字を扱っており、生活に役立っているのである。その中で最も利用者が多いと思われるのが、「路線検索(鉄道の乗り換え)」サービスや、カーナビの「ルート検索」だ。東京や大阪などの大都市圏の鉄道網、都市部の道路の複雑さなどを思い浮かべれば、最寄り駅(現在地)から目的の駅(目的地)まで行くのに、どれだけ膨大な組み合わせがあるか想像できるだろう。

もしかしたら、最適ルートなんて、「最も時間がかからないか」、「最も安いか」、「最も乗り換え回数が少ないか」の3つの条件で1つ2つぐらいしかないから、天文学的な数になるわけがない、と思うかも知れない。

ところがどっこい、それは全体を見て俯瞰できる人間だからできる考え方であって、コンピュータは1駅ごと、1交差点ごとに確かめていかないと、どんなルートがあるのかわからないし、どれが一番適したルートなのかも確かめられないのである。普通なら利用しないあり得ないルートも含めると、その数は膨大になり、天文学的な数にまでふくれあがってしまう。よって、ムダなルートを省く「圧縮技術」が重要となってくるのだ。

そのほかにも、組み合わせといったら、日本の歴史あるテーブルゲーム「将棋」や「囲碁」などもすごい。対局で現れる局面の数は、将棋で10の70乗通り、囲碁に至っては10の170乗通りもあるのだそうだ。10の70乗は「100無量大数」ということでなんとか日本の一般的な数の単位で数えられるが、10の170乗などというのはお話にならない(仏教で使われている日本では一般的ではない123個の単位を使えば、最大の「不可説不可説転」が10の37澗2183溝8388穣1977じょ6444垓4130京6597兆6878億4964万8128乗ということなので、余裕で数えられる)。

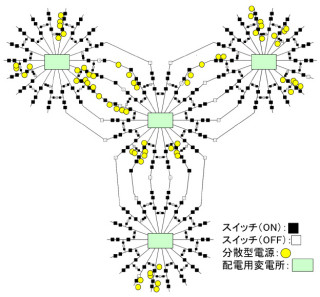
そのほか、不可思議級の組み合わせが発生しているのが、電気の配電網だ。これについては、2月24日に当サイトで、湊博士も関わった研究成果として「早大など、スマートグリッド用の効率的な送電を実現するアルゴリズムを開発」という記事を掲載したので、こちらも併せて読んでいただきたい。

かいつまんで説明すると、日本の実用規模の標準的な配電網モデルでは、制御可能なスイッチの数が468個、その組み合わせの総数は141桁になるそうで、これまで世界中のどの国でもこうした大規模な送電網の正確なルートの組み合わせの総数などはカウントされたことがなかったのだという。

そして、研究で開発されたアルゴリズムを用いて、送電損失を削減できる条件を満たす組み合わせの総数をカウントしたところ、「2136那由他8201阿僧祇3834恒河沙8532極9116載8261正2214澗8049溝560穣9817じょ8392垓4438京5235兆3981億8952万1540通り」だったそうだ。この規模で1の位まで正確にカウントしたのは、世界初ということである。

でも、スーパーコンピュータの京などを使えば、このぐらいの組み合わせは、1つひとつ確かめていく力任せの計算でもそんなに時間をかけずに出せるのでは? などと思うかも知れない。が、驚くなかれ、この規模の組み合わせになってくると、何もしない力任せの計算では答えが出るまでに何1000年とかかってしまうこともあるのだ。そこで必要となるのが、前述したように、ムダを省くための圧縮技術となるのである。今回は、その計算の技術や、その技術によって我々の未来がどう変わるのかも体感できる内容となっている。

コンテンツは全部で5つ、順を追っていく5段階で紹介されており、「とにかく数え上げるべし!(見習い)」、「爆発を感じるべし!(門下生)」、「「圧縮」の極意を知るべし!(初段)」、「奥義「圧縮」炸裂!(師範代)」、「「圧縮」が切り開く未来(師範)」という構成となっている。

最初の「とにかく数え上げるべし!(見習い)」は、数が増えてくると労力がどれだけ増すかということがわかる。でも、すべてを数え上げることも重要であり、重複や漏れなくすべてを数え上げるためにはどんな工夫ができるか、またヒトとコンピュータの数え方の違いにも注目する内容だ。

具体的には、画像6のような図形を用いて、左上の頂点から右下の頂点まで、同じ辺や線は2度通らずにゴールするという問題に挑戦し、何通りのルートがあるかを答える。人間、自然と最短ルートを通ろうとするから遠回りルートは意外と見逃しがちで、なるほど、と感心できる解答だったりするのだ。

普通、画像6のような図形の場合、上回りのA→F→I→Jとか、下回りのB→E→H、中央を通るA→C→D→Hなどをすぐ思いつくだろう。でも、全ルートを見出そうとすると、ヒトが持っている「ゴールへ一直線に向かう」という先入観を捨てないとならない。同じ線を2回通ってはならないというのが条件であって、「最短で」とは設定されてないのである。果たして、何通りあるのは、ぜひ未来館で確かめてみよう。

そして次の「爆発を感じるべし!(門下生)」は、数えるものが少し増えるだけで、その組み合わせはまさに爆発的に増えていくというのを実感できるコーナー。例として、見習いコーナーの画像6と似ているが、縦横同じ数だけ並べられたマス目の組み合わせを用いて、そのすごさを表している。同じように、同じ辺や線は2度は通らないという条件の下、左上の頂点から右下の頂点まで目指すルートをすべて数えるのだが、まさに数字の爆発を見られる。

1マスの場合は辺が4本でルートは2通りだが(画像7)、これが2×2マス(画像8)になると、辺と線の合計が12本に増え、ルートも12通りに。さらに3×3マス(画像9)になると24本になって184通りと、一気に増えていく。

そして16×16マス(画像10)になると、マスの数は256個、辺と線の数も544本と、それほど多くないのだが、組み合わせは……。前述した日常生活ではまず縁のない上の方の単位の数字が普通に出てくるので、その数字が爆発的に増加するところと、どれだけ大きな数字になるのかを見てほしい。

ところで、16×16マスのような複雑なものになってくると、その組み合わせは天文学的な数字になるので、スーパーコンピュータですら何1000年もかかってしまうと書いたが、ならなぜ実際に解答を出せているのか？　どうやって短時間で導き出したのかが、気になるところである。

それを答えてくれるのが、「「圧縮」の極意を知るべし!(初段)」のコーナーだ。先ほど少し触れたが、ムダを省く「圧縮技術」についての解説が用意されている。この圧縮技術があるから、現代のコンピュータでも16×16マスという驚くほど複雑なルート計算の正確な答えも出せるのである。

組み合わせのムダを省くというのは、どんな話かというと、例えば、話をできるだけ簡単にするため、2×2マスで説明してみよう。左上から順に線ごとにはアルファベットをふって名前をふってある(画像11)。

コンピュータの場合、交差点にくる度にすべての方向に対して調査を行うので、例えば、AとCの間の交差点に来た時、そのまま直進してCに進むのと、Dに進むのは問題ないが、ムダなAに戻るコースなども1度調べてしまう。しかし、交差点ごとに全ルートを調べるという力技でも疲れ知らずで行えるため、ヒトが逆に苦手とする「最短じゃないルート」をいくつも見つけられるというわけだ。

しかし、この総当たりで確かめるのはムダがある。最初から絶対にあり得ないルートがあるからだ。つまり、圧縮とは、そうしたあり得ないルートを削除してしまうことで、それだけ少ない計算で導き出せることになる。

例えば2×2マスの場合(どれもそうなのだが)、絶対に辺AかBからスタートするわけで、当たり前だがC～Lが最初になることはない。また、Aからのルートを選んだら絶対にBは通らないし、逆にB→Aもない(ゴールへ向かえないので)。また、AからいきなりEといった線が直接接していない組み合わせもあり得ない。そしてルートの最後は、絶対にゴールの頂点に接しているKかLの2辺のどちらかになるわけで、それ以外もあり得ない。

こんな感じで、Aでスタートしたら、その次はCかD、Dを選んだらE、I、H、最後はKかLという具合にあり得るルートのみを残して、ダメなものをどんどん削っていくと、カウントする数が減っていく(画像12)。2×2マスだとそれほど劇的ではないが、もっとマス目の数が増えてくると、一気にバッサリと多量に削れるから効果も絶大になる(もちろん、可能なルートの総数も膨大になるのだが)。

そうすることで、力任せに確かめていくスタイルだったらスパコンですら何1000年とかかってしまうような先ほどの電力網の最適ルートも、2時間20分ほどで済んでしまうというわけだ。

圧縮の考え方を学んだところで、実際に組み合わせの数がどう変化するのかを体験できるのかが、次の「奥義「圧縮」炸裂!(師範代)」だ。世の中、何でもかんでもバッサリ切り捨てて合理化すればいいというものではないが、自分の生活やビジネスなどのさまざまな場面で、こうした効率化の考え方が役に立つ場面があることを感じるはずだ。ぜひ、自分の目で体感してみよう。

そして最後の「「圧縮」が切り開く未来(師範)」は、湊博士のように計算の効率化などのアルゴリズムの研究をしている研究者のコメントが掲載されている。「なるほど」をいくつも感じられるはずだ(画像13)。

なお、湊博士は内覧会の挨拶で、今回は若い研究者たちの研究内容も取り上げているので、この第11期展示をもっと若い、中高生たちにも見てもらって、ぜひ将来、そうした中からこうした数学やプログラム、アルゴリズムといった世界に興味を持って研究してくれる人が出てくれれば嬉しいということを語った。

また、個別に話を伺ったところ、湊博士がこうした数学やプログラム、アルゴリズムの世界に興味を持ったのは、10代前半の頃まで遡るそうだ。まだパソコンが世の中に出るか出ないかの時代、ワンボードマイコンでいろいろと作っては分解して遊んでいたそうだが、それからパソコンが普及しだして、ソフトウェア的にほぼ同等のことを行えて、しかもハードウェアと異なってすぐに修正や改良など手を加えられることから大変感動して、それ以来この世界にどっぷりハマっているということである。

さらに、驚くべきことに、筆者(の記事)と今回の第11期展示についての接点も教えてくれた。実は前述した当サイトの2月24日付けの筆者の記事で、日本の単位を付け足したたことが、今回の展示の見せ方のヒントになったという。記事作成時に参照した元々のプレスリリースには漢字の単位は入っておらず、ただ数字の羅列だったのだが、たまたま筆者は数字の単位が好きだったものだから、見やすいだろうとして入れてみたのだが、それが湊博士の目に留まり、「この手があったか!」となったそうである。

大げさな話だが、筆者が単位を入れていなかったら、第11期展示の内容は変わっていたかも知れないということで、何はともあれ、自分の記事が役に立ったという話を聞かせてもらえるのは、ライター冥利に尽きるというものだ。

こんな感じで、日本の数の単位が全部で21もあること、そんな膨大な数が実は身近にあるということなどを知ることのできる今回の展示。内容的には中高生から上という感じだが(四半世紀前だが、筆者は高校3年生の時、理数系の選択コースで確か習ったような気がする)、小学生でも「聞いたことがない数字の単位」というのは、興味深い題材だと思う。

お子さんに算数や数学に興味をもっと持たせたいと考えている親御さんは、ぜひこの機会を利用してもらいたい。やっぱり、勉強は「なんでだろう?」とか「これって面白い」があってこそその教科を好きになれて、さらに成績も伸びると思うので、ぜひ今回の展示を活用することをオススメする。