NIMS、物質の状態が変化するきっかけの「核生成現象」の新たな過程を発見

物質・材料研究機構(NIMS)は2月22日、物質の状態が変化するきっかけとなる現象である「核生成現象」について、これまで知られていない新たな過程があることと、それを説明する理論を発見したと発表した。成果は、NIMS理論計算科学ユニットの西野 正理主任研究員らの研究グループによるもので、論文は「Scientific Reports」オンライン版にて2011年11月22日に公開済み。そのアブストラクトの和訳が、日本語Webサイトに「注目の論文」として2012年1月23日に掲載されている。

核生成は、気体や液体の凝縮や凝固において、あるいはある磁気的な状態から別の磁気的な状態へ転移する現象である「磁気転移」や「強誘電転移」などの「ヒステリシス現象」などにおいて起こる現象であり、1つの相から別の相へ変化する現象である「(1次)相転移」(例えば凝縮や蒸発は液相と気相の間の相転移で、固相間の相転移には磁気転移、超伝導転移、構造相転移などがある)を起こす系での安定状態(平衡状態)とそれに準じた「準安定状態」の間で起こる普遍的に見られる現象だ。核生成研究は、エレクトロニクス技術から気象学に及ぶ広範囲な研究分野において重要なテーマである。

なおヒステリシス現象とは、ある量の大きさ(Y)が他の量(X)の変化に伴って変化する時、Xの変化の経路によって同じXに対するYの値が異なる現象のことをいう。Xの関数としてYのグラフを表した時にグラフが閉曲線になる場合、ヒステリシスループ(画像1)と呼ぶ。例えば強磁性体の場合、Yは磁化でXは外部磁場に相当する。

鉄系錯体の結晶などに多数報告されている、大きなスピンを持つ状態(高スピン状態)と小さなスピンを持つ状態(低スピン状態)が競合するため、温度や圧力の変化、光照射、磁場印加などで異なるスピン状態に転移する物質系である「スピンクロスオーバー化合物」では、Xは温度や圧力、YはHS(LS)相の割合、磁化、体積などだ。

また準安定状態とは、準安定状態と安定状態の間には、乗り越えるべきエネルギー障壁が存在し、ここでは特に熱力学的平衡状態(最安定状態)を考えた時、それに準じる安定な状態を指す。

核生成は、伝統的にミクロな現象と考えられている。「準安定相」中に現れる安定相の核を構成する「粒子集合体(ドロップレット)」の表面は(自由)エネルギーの増加をもたらすのに対し、内部は減少をもたらす(画像2)。

空間次元が3次元(2次元)ならば表面のエネルギーは粒子集合体の半径の2乗(1乗)で増加し、内部のエネルギーは3乗(2乗)で減少する。この表面と内部のエネルギーの競合によりエネルギーバリア(活性化エネルギー)が生じる具合だ。

画像2のグラフは、横軸が粒子集合体の半径で、系の空間次元をdとすると、表面のエネルギー(半径のd-1乗で増加)と内部(バルク)のエネルギー(半径のd乗で減少)の競合により、エネルギーバリアが生じる。バリアにおける粒子集合体が臨界核である。その半径(rc)は物質の種類で決まる特定の値を持つ。

バリアの頂点に対応する核を「臨界核」と呼び、安定相の粒子集合体が熱揺らぎなどによりそれがより大きくなると、自発的に核が成長し、相変化が起きる。物質の種類が決まれば、臨界核の大きさはある特定の値を持つと考えられており、例えば、さまざまな金属の凝固における核(臨界核)の半径は1nm程度と見積もられているというわけだ。

なお臨界核とは、準安定相から安定相への移行過程で、安定相の粒子集合体がそれ以上成長するか消滅するかを分ける臨界的な大きさが存在し、その臨界的な大きさを持つ粒子集合体のことをいう。核生成とは、簡単にいえばこの臨界核の発生により安定相へ変化する過程のことである。

この考察は、厳密には分子(要素)間に働く相互作用が遠くの分子に及ばない場合(短距離相互作用)に正しい。この場合、表面と内部のエネルギーの寄与が分離でき、臨界核の大きさは特定の微視的な値になる。核生成理論は、この仮定を基礎としているが、相互作用が遠くに及ぶ場合(長距離相互作用)は、その仮定が成り立たない可能性があり、既知の核生成とは本質的に異なった性質やメカニズムが存在し得る可能性があった。

スピンクロスオーバー化合物などの分子性結晶においては、温度や圧力、あるいは光照射などの環境の変化によって非磁性状態と磁性状態の間で相転移することが知られている。

相が変化する時、系の大きな体積変化を伴う。結晶を構成する分子(錯体分子)は、電子状態と分子サイズに関して2つの安定した状態である「双安定性」を持つ。つまり、高温では高スピン(HS)状態を取り大きな分子サイズであるが、低温では低スピン(LS)状態を取り小さな分子となる。この系においては、分子の大きさが変化することで起こる「格子ひずみ」が原因となって分子間に弾性相互作用が働く。

この弾性相互作用が「協力的相互作用」となって相変化をもたらす。物質を構成する個々の要素(例えば、分子や磁性体のスピンなど)の間の相互作用が協力的に働くことにより、個々の要素単独では見られない、質的に新しい現象を示すことを協力現象といい、その典型が相転移である。この協力現象において個々の要素の間に働く相互作用のことを協力的相互作用という。

今回、この相互作用についての考察がなされ、分子の体積(大きさ)変化を扱った弾性相互作用のモデル化を行い、核生成の特徴に関しての理論的な研究が行われた。研究グループのこれまでの研究から、この弾性相互作用は長距離に影響することがわかっており、相互作用の長距離的性質が核生成過程に及ぼす影響が注目された次第だ。

2次元の円盤型結晶を考え、低温で準安定状態であるHS相(赤色部分)から安定相のLS相(青色部分)への緩和で起こる核生成過程を、分子動力学法を用いて調べたのが画像3と4である。

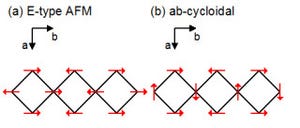
画像3は、準安定相(赤色)から安定相(青色)への緩和過程におけるスナップショットだ。aの系(2R=200分子)とbの系(2R=100分子)では、全系(円盤)の直径(2R)は2倍異なる。aとbの系において、同じ番号(1～6)のスナップショットは、青色部の割合が同じ。a1とb1の青色部分は臨界核に相当し(画像4参照)、核生成と成長のスナップショットはシステムサイズの異なる系において、相似形を示す。

そして画像4は、まず(a)が準安定相(赤色)において角度θで特徴づけられる安定相粒子集合体(青色)。画像3の緩和過程の粒子集合体(青色部分)は、ここで定義するθをパラメータに取ると、よく近似できる。青色部分は半径rdの円の一部。

そして(b)は、角度θで特徴づけられる粒子集合体が存在する場合の全系のエネルギー密度。エネルギー密度は粒子あたりのエネルギーで、完全な準安定相(θ=0の時)を基準に取る。Δρ(θ)=ρ(θ)-ρ(0)。ρ=E/N(Eは全系のエネルギー、Nは全粒子数。N≈πR2乗)グラフの横軸はθ/π。異なる大きさの系(2R=100,200,300)において、エネルギーバリアを与えるθ/π(=2.3/10)は不変であることに注意。ここでは臨界核の臨界半径(rc)は存在せず、臨界角(θc)が存在する。この時、青色部文は全体の5%。すなわち、臨界核の大きさは、全系の大きさに相対的なものになるというわけだ。

その結果、臨界核の大きさには絶対的な値は存在せず、臨界核は全系の大きさに比例して大きくなり、系の大きさに対して相対的なものであることが明らかになった。

これは、この格子ひずみによる長距離的相互作用がもたらす効果であり、短距離相互作用の場合と異なり、もはや表面のエネルギーとバルクのエネルギーは分けることができないという事実を反映している。

この現象は、これまで知られている核生成の概念とは異なり、核生成はさまざまなスケールで実現し得ることから、巨視的な過程にもなり得るため、ここに「巨視的核生成」という新しい核生成の概念が提案できるというわけだ。

今回の研究での成果は、これまでの核生成理論の枠内では捉えられない現象を解析したことで、核生成の未解明な問題に対して有用な知見を与えると考えられると、研究グループはコメント。

格子歪みによって伝えられる弾性相互作用が長距離に及ぶ系の核生成機構の進展が期待できるともいう。例えば、形状記憶効果に密接に関係する「マルテンサイト変態」(原子の拡散を伴わず、(擬)せん断変形的に起こる固相中における構造相転移の1種)、磁性体を磁化するとそれが変形する現象の「磁歪(磁気ひずみ)」、「ヤーン・テラーひずみ」(ある状況下で分子の対称性が下がり、電子のエネルギー準位の縮退が解けて安定化された状態が実現されるが、この時に分子の構造が変形して歪む現象)による構造相転移などの未解明なメカニズムに対して有用な知見を与えると考えられるというわけだ。

今回の知見は、結晶を構成する分子の大きさが双安定性を持ち、温度、圧力などの環境の変化で分子の大きさや形状が変わる系においては、広く適用することができる。画像4において、エネルギー密度が系の大きさを変えてもほとんど変わらないので、全系の大きさ(2次元系の場合は系の面積、3次元系の場合は系の体積)に比例してエネルギーバリアが増加する形だ。

すなわち、準安定性の強さは、系を大きくすると著しく増加するので、例えば、光メモリなどのスイッチングデバイス設計において、準安定状態の強さ(記録保持時間)を制御したり、ヒステリシスループの幅を拡げたりすることが、物質の種類を変えずに系の大きさのみを調整することで実現する原理が与えられるというわけである。