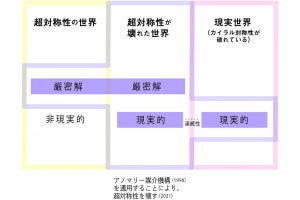
理化学研究所(理研)は9月1日、周期的に駆動された「量子多体系」において、「隠れた反ユニタリー対称性の自発的破れ」に起因した新しいメカニズムによる動的な相転移現象を発見したと発表した。
-
今回の研究が結びつける分野の模式図。非平衡ダイナミクス、量子多体系の相転移、非ユニタリー行列の数理を結びつけるものである (出所:理研Webサイト)
同成果は、理研 開拓研究本部 非平衡統計力学 理研白眉研究チームの濱崎立資 理研白眉研究チームリーダーらの研究チームによるもの。詳細は、英オンライン科学誌「Nature Communications」に掲載された。
温度などの外部パラメータを変えることで、系のマクロな性質が劇的に変化する現象を「相転移」といい、熱平衡状態にある系の相転移現象(平衡相転移)の研究は長い歴史を長く、そのメカニズムや相転移点近くでの普遍性についての理解は進んできている。一方、非平衡状態において、相や相転移をどのように特徴づけるかも重要な問題とされながらも、平衡相転移と比べると未開拓な状況だという。
そのような非平衡下での相転移の中で注目されているのが、平衡状態の自由エネルギーに含まれる温度のパラメータを時間に置き換えた「動的自由エネルギー」の特異性から定義される「動的量子相転移」と呼ばれるクラスの相転移だという。
物理的には、動的自由エネルギーは「ある状態を量子的に時間発展させた状態」と、「別の参考状態」がどれほど重なっているかの指標になっているとされるが、動的量子相転移の理論的・実験的な研究が進められている一方、そのメカニズムや普遍性についての理解は進んでいなかったという。
こうした背景を受けて行われた今回の研究で発見されたのが、周期駆動された「(一次元)量子イジング模型」における、「隠れた反ユニタリー対称性の自発的破れ」に起因した新しいメカニズムの動的な相転移現象だという。量子系がある作用を施しても変化しないとき、その作用を対称性と呼び、その変換の際に複素共役を取る操作が含まれるのが反ユニタリー対称性だという。
今回の研究では、量子イジング模型における動的自由エネルギーの回転角を変えると、典型的な動的量子相転移とは異なる、強い特異性を持つ動的量子相転移が起こる場合があることが発見された。
-
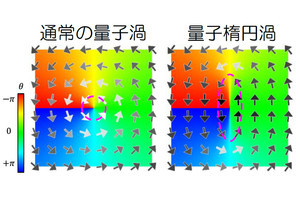
周期駆動された量子多体系と時空間双対性の概念図。周期駆動された量子多体系とその時空間双対性。左図のように、一次元空間にあるスピン(矢印で示されている)が1周期ごとにユニタリー時間発展し、一定時間後に動的自由エネルギーが測定される。時空間双対性では、右図のように、空間と時間の役割を入れ替える。つまり、時間方向に広がったスピンが空間的に伝搬すると見なす。これにより得られる空間伝搬の操作は、非ユニタリーな行列で記述される。この非ユニタリー行列が反ユニタリー対称性の破れを起こすとき、動的自由エネルギーの強い特異性が現れる (出所:理研Webサイト)
典型的な動的量子相転移では動的自由エネルギーの回転角に対する変化量は有限の跳びを示すだけだが、今回発見された動的量子相転移ではこれが発散することが特徴だとする。
-
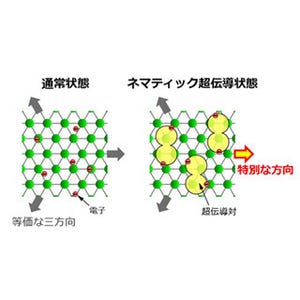
動的量子相転移(左)と反ユニタリー対称性の破れ(右)の概念図。今回発見された動的量子相転移と反ユニタリー対称性の破れ。スピンの回転角(外場の強さ)を変化させると、転移点(II)において、動的自由エネルギーの変化量が発散するという強い特異性が現れる(左図)。この相転移は、右図のように、時空間双対後の非ユニタリー行列の「反ユニタリー対称性の破れ」から説明される。すなわち、回転角を変えると行列の固有値が例外点を通り、これが転移点での発散を説明するという (出所:理研Webサイト)
この発散の起源と普遍性を調べるために、今回の研究では時間と空間の役割を入れ替える「時空間双対性」という理論的手法を採用。そこから、空間的変化の伝搬は、通常の(ユニタリーな)量子力学の時間発展と異なり、「非ユニタリー」と呼ばれるクラスの行列によって記述されること、ならびに非ユニタリー行列が元の模型の相互作用が適切な値のときに、反ユニタリー対称性を持ち、その際、パラメータの変化に伴い「対称性の自発的破れ」が起こり得るということが示されたという。
非ユニタリー行列の反ユニタリー対称性の自発的破れは、通常の平衡相転移には見られない特異点である「例外点(固有状態が重なる点)」を伴うことが知られており、今回の研究では、この例外点の振る舞いが、元のモデルでの動的自由エネルギーの変化量の発散を説明するということが示されたともする。
今回の成果について研究チームでは、非平衡かつ非定常な状態に対しても量子相およびその転移が定義され、そこに対称性の破れや普遍性などの概念が存在することを示すものであり、今後こうした動的な量子相を分類するための1つの指針になることが期待されるとしている。また、今後は、今回の研究で導入された概念や手法を通じて、量子多体系のダイナミクスの理解が進むことが期待されるともしている。
