“不気味な遠隔作用”こと「量子もつれ」に関する新たな法則を理研と慶應大が発見

理化学研究所(理研)と慶應義塾大学(慶應大)は9月8日、量子力学的に運動する多数の粒子系である「量子多体系」において、最低エネルギー状態(基底状態)が持つ「量子もつれ」に関する新たな法則を発見したと発表した。

同成果は、理研革新知能統合研究センター汎用基盤技術研究グループ数理科学チームの桑原知剛研究員と、慶應義塾大学理工学部物理学科の齊藤圭司教授の共同研究チームによるもの。詳細は、オンライン科学誌「Nature Communications」に掲載された。

量子力学の世界には、まるで光の速度を超えるどころか、どれだけ距離が離れていても無限大の速度で情報が伝達しているかのような不思議な現象がある。それが量子もつれ(量子エンタングルメント)だ。かのアインシュタインは量子もつれのことを「不気味な遠隔作用」と呼んで、量子力学そのものも含めて毛嫌いしたという。

量子もつれを利用すれば、光速を超えた情報伝達が可能となるかもしれないと考える研究者もおり、物質転送や超光速通信など、SF作品に登場するテクノロジーを実現するカギとして研究が進められている。それと同時に、量子コンピュータによる量子計算においても重要な役割を果たしており、「不気味な遠隔作用」はすでに現実でも利用される段階にあるといえる。

このような奇妙な性質を持つ量子もつれだが、コンピュータシミュレーションを含むこれまでさまざまな解析から、多数の粒子が集まった一般の量子多体系における最低のエネルギー状態=基底状態が持つ量子もつれの大きさは、高エネルギーの状態と比較すると格段に小さいと予想されている。

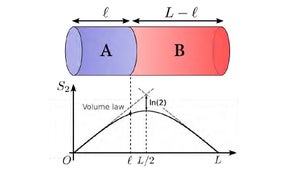
量子もつれの大きさを示す物理量として「エンタングルメントエントロピー」があるが、これは多体系を半分に切ったときの領域AとBの間にある境界の面積にほぼ比例するという。そして、それ以上には大きくならないことから、領域AとBの間の領域もつれの大きさは、境界の大きさとほぼ同じであるという特徴を持つ。そのため、この予想は「領域もつれの境界則予想」あるいは「領域もつれの面積則予想」と呼ばれており、コンピュータシミュレーションを用いて量子多体系を研究する際の重要な性質として研究されている。

量子もつれの境界則予測は、これまでは粒子間に働く相互作用が小さく、粒子が独立に運動しやすい(短距離の相関がある)状況では、数学的に証明されている。しかし、相互作用の種類や大小によって、境界則成立の可否がどのように左右されるのかは、未解決問題の1つとなっていた。この問題を解決することは、量子もつれに関する理解が深まることに加え、量子多体系を用いた情報処理演算の効率化にも直接的につながる重要な波及効果が期待されることから、研究チームは今回、自然界に働くもっとも一般的な相互作用を採用し、この問題に取り組むことにしたという。

自然界には、重力や、電子間に働くクーロン力、水分子のような極性分子の間に働く力、ミクロな磁石の構成分子の間に働く力など、遠くまで到達する力(長距離力)が存在する。研究チームはまず、長距離力で相互作用し、基底状態とエネルギーが高い状態との間に有限のエネルギーギャップがある1次元系を考案。長距離力がもたらすポテンシャルの大きさは、距離に対して“べき乗則”に従ってゆっくりと小さくなる。そして、距離rの関数として「r-α乗(αは乗数で、正の定数)」で表される。

一般的に、量子多体系における基底状態を正確に調べることは、難しい数学上の問題の1つとされる。そのため、研究チームは基底状態を近似的に求めていく手法として、低いエネルギー状態を特定の状態に逐次「射影」していく手法「Approximate ground-state projection」を用いることにしたという。射影とは、ある量子状態がさまざまな状態の重ね合わせにあるときに、特定の状態に収縮させる操作のことをいう。

ただし、射影行列(射影操作の数学的表現)を領域AとBの2つの領域の間の量子もつれの大きさが小さくなるような行列で表現することと、逐次射影による基底状態の近似計算の精度は、トレードオフの関係にあり、この問題について研究チームは、射影行列の構成を最適化すること、高いエネルギー状態を効率良く無視するための特定の問題に対して現象をよく説明でき、かつ簡潔に記述された系のエネルギーに対応する関数「有効ハミルトニアン」を導入することで克服することに成功したという。ハミルトニアンとは系のエネルギーに対応する関数のことで、有効ハミルトニアンは、

これらの数学的な手法を用いて、1次元系においては、一般的に「α＞2」のときには、量子もつれの境界則が満たされることが見出された。さらに、量子多体系が「2次形式」で書き下ろすことができる数値的に可解な系では、「α＞3/2」でも境界則が満たされることが確認された。これらの結果は、これまで境界則に必要と考えられていた相互作用の短距離性の条件が本質ではないことを示しているという。そして、強く長距離まで届く相互作用があっても、境界則が成立することが初めて明らかとなったとのことで、これにより、量子もつれの境界則が広範囲な量子力学系で存在することが確認されることとなったとする。

量子もつれの境界則が広範囲な量子力学系で存在するということは、広範囲の系で、基底状態を探る数値計算を探索できることを示しているという。さらに今回の成果は、境界則成立が重要になる「テンソルネットワーク」を使った量子アルゴリズムや、量子計算、量子機械学習など、多くの分野に知見をもたらすことが期待できるとしている。