球面調和関数とはなにか?
「球面調和関数」は言葉の響きが難しいので、まずはイメージから捉えよう。
球面調和関数とは、かなり極端に簡略化して説明すると、球っぽいモノから任意の長さの針が突き出た「いびつなウニ」みたいな物体の形状を数学的な関数で表すためのもの……といえる(ウニの針が逆に凹んでいる場合もある)。
これがどうしてキューブマップの圧縮に使えるのかイメージが湧きにくいかもしれない。
順番に説明していこう。
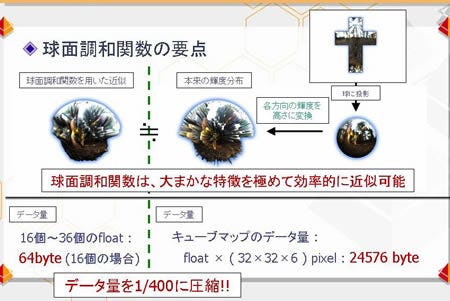
全方位の情景を表したキューブ環境マップを球に見立て、そのキューブ環境マップのテクセル(画素)の値を"高さ"に見立てる。すると「いびつなウニ」みたいな立体ができあがる。そして、このいびつなウニを正確に記録するのは諦めて、「大体の形状」を記録する方針に変更する。その手段として球面調和関数を用いるのだ。
先ほど、32×32テクセルの6面体のキューブ環境マップの例を出したが、非圧縮では1頂点あたり24kBのデータ量であった。記録する球面調和関数の係数の個数でデータ量が変わるのだが、実用レベルで16個程度でも十分といわれる。例えば仮に16個の32ビット浮動小数点とすればわずか64バイト。24kBの1/400に小さくできることになる。先ほどの4万頂点の例で行けば、2.4MBで済むことになり、938MBと比べればかなり現実的なデータ量に圧縮できる事が分かる。
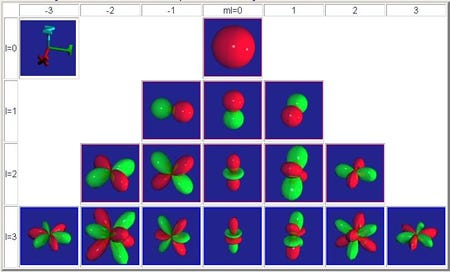
球面調和関数は、ある形状を表現するのに複数の関数群から成り立っている。その関数の数が多いほど形状表現が正確になる。詳しい数学的な定義はここでは省略するが、下図に、あるパラメータを与えられた球面調和関数を示す。この図において上から1段目までの球面調和関数を用いれば1個、2段目までを使うならば合計4個、3段目までを使うならば合計9個、4段目までを使うならば合計16個……という具合に関数は増加する。
図をもう一度見て欲しい。
lの値が小さい時ほど形状が単純で、逆にlの値が大きくなると(下に行けば行くほど)トゲトゲして形状が複雑になっている事が分かる。先ほどの「いびつなウニ」の形状を近似するにあたり、多くの球面調和関数を用いれば高品位に近似できると述べた。これはつまり、この図の下の方の複雑な形状までを用いれば用いるほど、その「いびつなウニ」を正確に表現できるということなのだ。
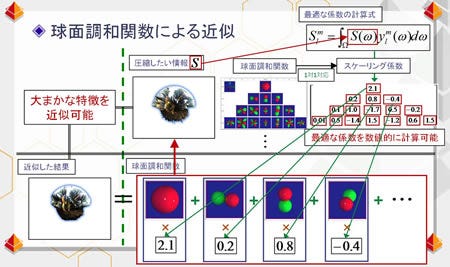
表現したい「いびつなウニ」は、キューブ環境マップであり、その値はキューブ環境マップごとに固有だ。ということは、それぞれそのトゲの長さやその球っぽい形の大きさが違う。あるトゲが長ければそのトゲが長くなるように球面調和関数の大きさを変えてやる必要がある。「いびつなウニ」形状の近似には、複数の球面調和関数に対して最適なスケーリング係数(大きさを決定づける掛け値)を与える必要があるのだ。この係数を求める計算はここでは省略するが、簡単に言えばある決められた方程式を解くことで求められる。
例えば、l=3までの16個の球面調和関数を用いて近似する際には16個のスケーリング係数を求める必要がある。
|
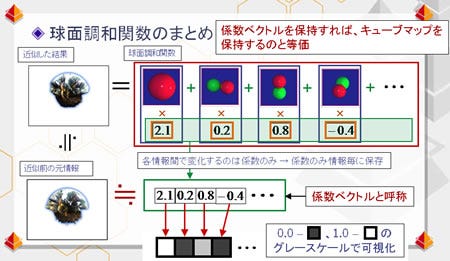
スケーリング係数を導出してしまえば、これだけで近似した「いびつなウニ」形状の復元が行える。なお、経験則的に、リアルタイム3DグラフィックスにおけるPRT用途の場合、大体16個(l=3)~36個(l=5)の球面調和関数で十分ということが分かってきている |
球面調和関数そのものは既存のものであり、算術的に算出できる。であれば、ある「いびつなウニ」形状を記録&再現しようとした際(近似されてはしまうものの)、その求めた係数だけを記録しておけば復元可能だ。
例えば前出の一頂点あたり24kBものデータ量が必要だったあの形状データを、16個の球面調和関数で表現するとすれば、わずか16個の係数を保存しておけば復元ができる。球面調和関数で1/400に圧縮できるからくりはここにある。
より感覚的なたとえをすれば、球面調和関数とは、MPEGやJPEGの圧縮に用いられる離散コサイン変換の「球体バージョン」ということができるかもしれない。(続く)
(トライゼット西川善司)