静的PRTをリアルタイム実装するための妥協と工夫
これをリアルタイムに実装するためには、いくつかの妥協と簡略化が必要になってくる。 1つ目の妥協点は、「シーンの状態の固定化」だ。つまり、シーンに登場するオブジェクトが全く動かないと言うこと。これは「静的」PRTの「静的」たる所以でもある。
|
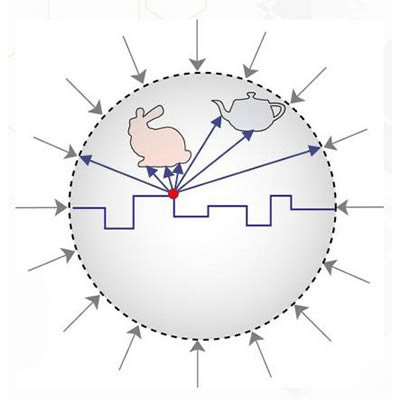
PRTでは、全ての頂点から全方位の遮蔽情報を事前に計算して取得、保持して活用するという基本方針を取る。よって、シーンに登場するオブジェクトが動いたら遮蔽構造をもう一度計算し直さなければならなくなるので、リアルタイム化にはシーンを固定化するしかない |
2つ目の妥協点は照明計算(陰影処理)を頂点単位とする簡略化だ。陰影処理をピクセル単位で行った方が高品位な映像が得られるのは当然なのだが、これを頂点単位に削減することで処理速度を稼ぐことができる。実際の処理系では3頂点の計算結果から、そのポリゴンを構成するピクセルカラーを線形補間して求めるというグローシェーディング的アプローチを取る。
ただし、頂点単位のライティングで注意しなければならないのは、レンダリング対象3Dモデルの頂点数(ポリゴン数)だ。
たとえ何もない平面の地面であっても、ここに第三者の影やその他の複雑な陰影が投射されてくることが想定されるので、1枚ポリゴンでなく多ポリゴンで分割して表現して行っておく必要があるのだ。これをせずに大ざっぱなポリゴン数だと陰影の結果が反映されず不自然になってしまう。
3つ目は、全頂点に対して事前計算した膨大な容量のデータを圧縮しようという方策だ。
例えば4万頂点のシーンで、キューブマップ化したIBL積分項が32×32テクセルの小さなキューブマップだったとしても、一頂点あたり32×32×6面×4バイト(αRGB各8ビットカラー)=24kB。これが4万頂点分あればトータルで938MBのビデオメモリが遮蔽情報の格納だけで使われてしまう。
これを圧縮する技術として用いるのが、近年3Dグラフィックスの世界で目にする機会が増えた「球面調和関数」(SH : Spherical Harmonics)だ。この球面調和関数とは「量子力学」の教科書に載っているような項目で、そうした特殊数学を3Dグラフィックスの世界に応用したというのがPRTのユニークかつ画期的な点だといえる。
ところで、全頂点の遮蔽構造を事前計算していたとしても、実は、IBL積分項から各頂点について全方位分の陰影演算を行うのは処理が重い。しかし、この球面調和関数を用いると都合よくその問題も解決できてしまう。(続く)
(トライゼット西川善司)












