Sandra 2015 SP2b Engineer Edition(グラフ15~32)
SiSoftware
http://www.sisoftware.co.uk/
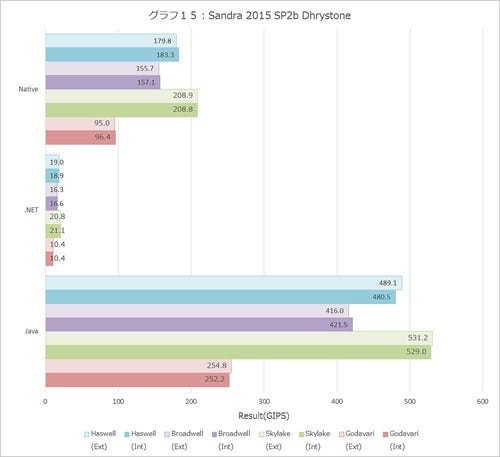
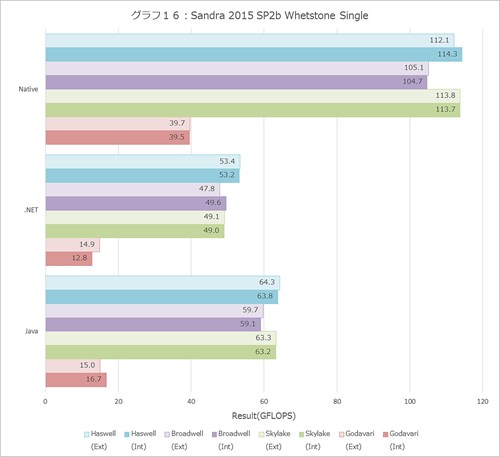
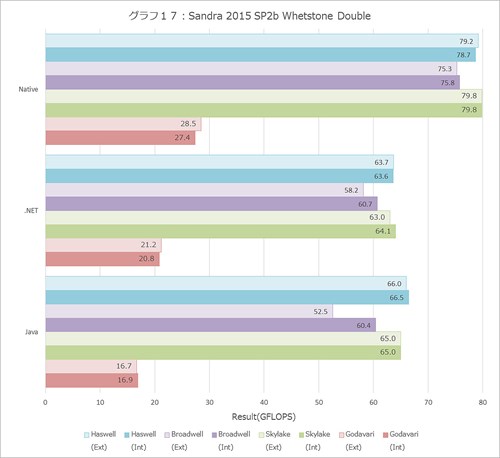
Dhrystone(グラフ15)の結果を見ると、こちらはおおむね10%前後の性能改善がきちんと出ており、ほぼ妥当な数字である。ところがWhetstone(グラフ16・17)ではHaswellと殆ど変わらない(というか、Javaの場合はやや性能が落ちている)という結果である。
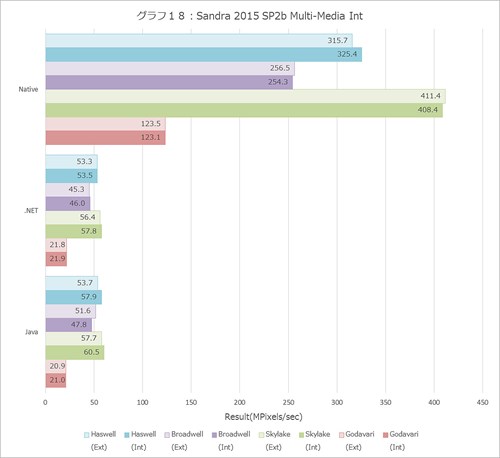
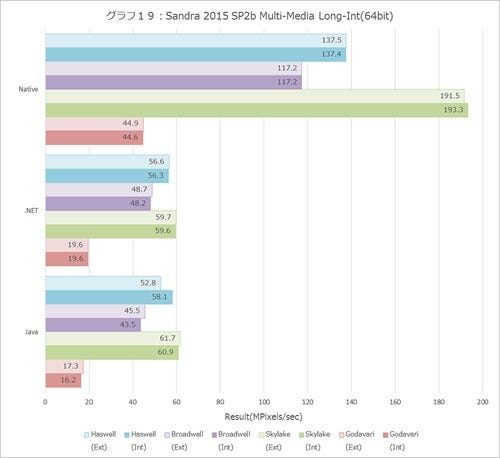
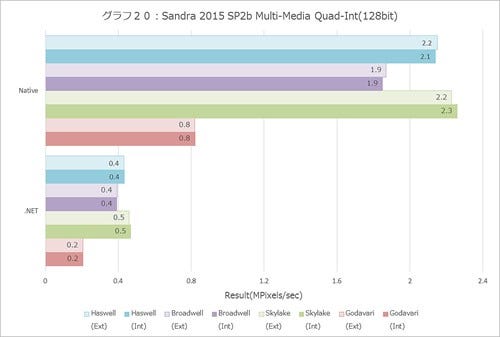
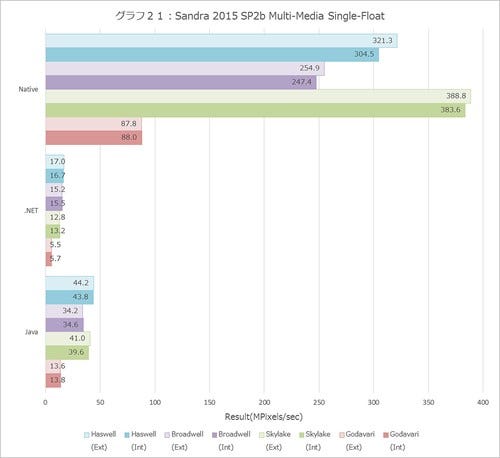
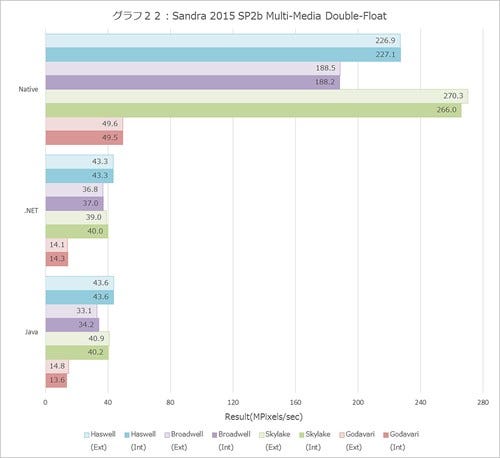
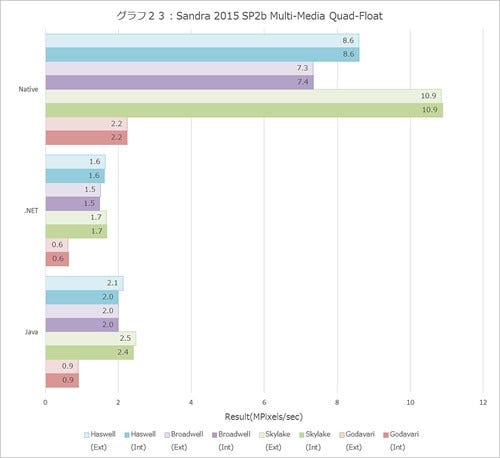
浮動小数点だと全部性能が上がらないのか? というとそういうこともない。Multi-Mediaの結果(グラフ18~23)をみると、Int系では10%どころではない性能改善が見られるし、Single/Double/Quad Float(グラフ21~23)も軒並み10%以上の改善が見られる。
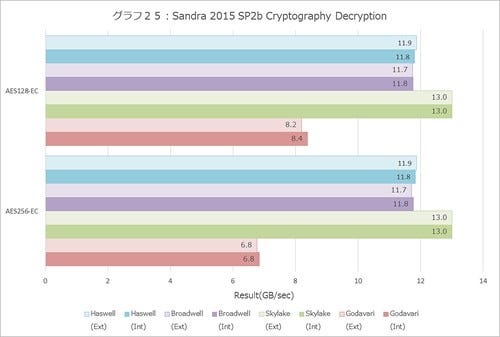
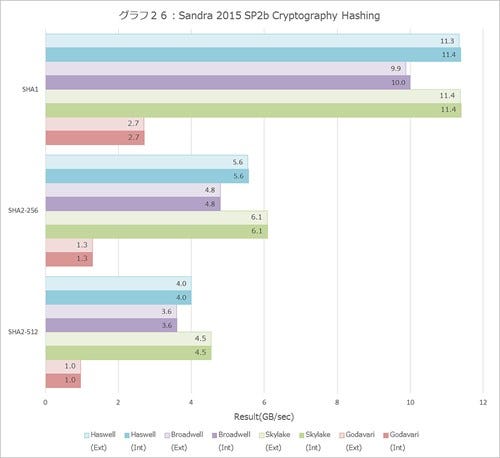
Cryptography(グラフ24~26)でもSkylakeの性能改善が明確に示されており、Hasing(グラフ26)では、SHA1の場合にデータ長が増えると性能が改善する傾向が読み取れる。
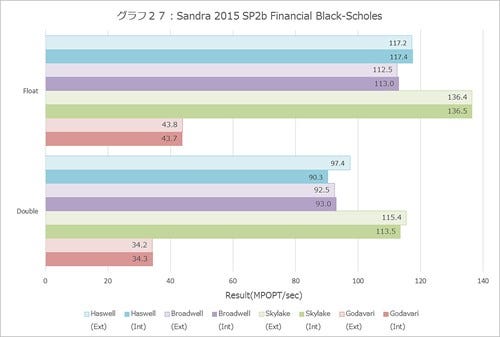
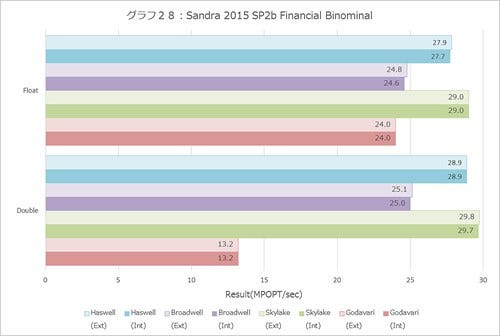
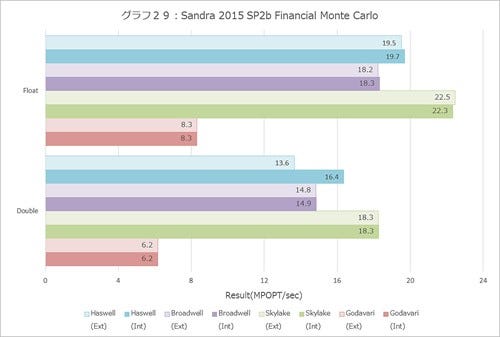
Financial(グラフ27~29)でもSkylakeの性能の高さは明確だ。10%まで行くかといわれればテストによって異なるが、Skylakeとそれ以外で明確に性能差が出ている。
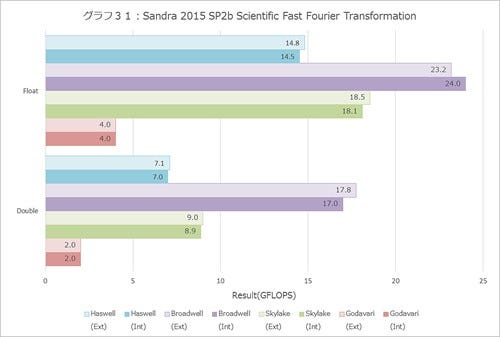
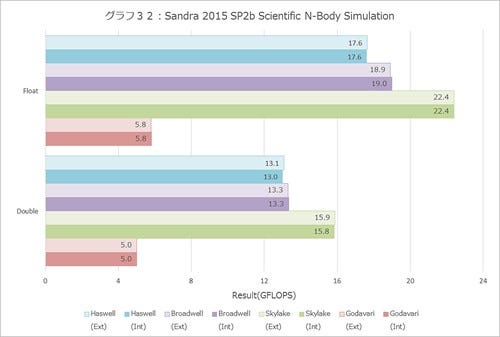
Scientific(グラフ30~32)も同じで、ランダムアクセス性能が最大のポイントとなるFFT(グラフ31)に関してはBroadwellに及ばない(これはL4が非常に効いているため)ものの、それでもHaswellに比べると明確に性能は改善しているし、GEMM(グラフ30)やN-Body(グラフ32)ではHaswell比で20%近い性能改善が示されている。
要するに、整数演算に関しては比較的単純に性能改善が得られるが、浮動小数点演算に関してはアプリケーションにかなり依存する部分があり、性能が落ちる場合もあれば上がる場合もあるという「謎の性能のバラつき」が露骨に示された結果となった。