CEDEC 2007 - NVIDIA、DirectX 10世代の流体力学技術とスキンシェーダについて解説

ナビエ・ストークス方程式を使用して流体物理シミュレーションを行う

さて、このNVIDIAのSmokeデモはどのように実現されているのだろうか。もうちょっと詳しく見ていくことにしよう。

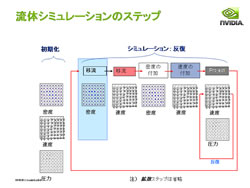
まず、流体物理シミュレーションを適用する領域を決めて、これを適当な解像度で仮想的に区切る。

例えばシミュレーション対象領域を縦100、横100、高さ100で区切ったとすれば、シミュレーション対象領域は100×100×100=1,000,000個の立方体に区切られることになる。

煙がたちこめる可能性がある領域全体をシミュレーション対象領域としなければならないので、広いシーンではこの区切り解像度を上げないとシミュレーションの精度は下がることになる。とはいえ、あまり高解像度に区切っても計算量やビデオメモリ使用量が増えてしまうのでバランスが重要になるわけだ。

細かく適当な解像度で区切られた単位立方体(グリッドセル、またはボクセルとよぶ)にはシミュレーション計算に必要なその時点での物理パラメータを格納しておく。

NVIDIAのSmokeデモの実装では、圧力、密度、水のシミュレーションの場合はそこが水なのか空気なのかを表す情報(液面境界情報)などをスカラ(単一の数値)で、そして速度をベクトル(x,y,zの方向性を持つ値)で各単位立方体ごとに持っている。

たとえば前出の100×100×100の例で行けば100×100の解像度のテクスチャを100枚用意し、その各テクセルに圧力、密度、液面境界情報、速度といった情報を格納していく。そう、ここまででも想像ができていると思うが、流体物理シミュレーションはテクスチャを大量に消費するのだ。

テクスチャに物理パラメータが入ったら今度は計算だ。この計算はGPUで行う。

「GPUは3Dグラフィックスをレンダリングするもの」という固定概念がある人には意味が分かりにくいかもしれない。実はプログラマブルシェーダ・アーキテクチャになってからは、GPUを計算器として、テクスチャメモリをデータテーブルやワークメモリとして活用することが一般化している。この例でもテクスチャに入れ込んだ各種物理パラメータをGPUでシミュレーション計算して更新していこうというアプローチになっている。

計算に用いる方程式は、コンピュータによる流体物理シミュレーションでよく用いられるナビエ・ストークス方程式(Navier-Stokes equations)を用いている。

数式は以下の図のようになる。

uは速度、tは単位時間、ρは密度、pは圧力を表す。一般ナビエ・ストークス方程式では粘性パラメータも考慮されるのだが、NVIDIA実装方式ではこれを無視している。余談だが冒頭で紹介した「鉄拳6」に採用された水面の流体物理シミュレーションでは粘性が考慮され、水面として維持されなくなった水粒は水滴として飛び散るようになっている。

さて、この数式、なにやら難しそうだが、最初の式は基本的には運動量保存則に基づいた運動方程式のF=maの「力F=質量m×加速度a」を変形した「a=F/m」(加速度=力÷質量)の形をしている。左辺の∂u/∂tは加速度で、右辺の第一項は移流項、第二項は圧力項、第三項は外力項となる。移流とは流れに従って動くこと、圧力は後述の非圧縮性条件を満たすように働く力、外力は風や重力などの外界からの干渉を表している。

「▽」はベクトル微分演算子で、ナビエ・ストークス方程式における「▽・u」は三次元ベクトルの場合、速度ベクトルu=(ux,uy,uz)とすると、

　　　∂ux　∂uy　　∂uz
▽・u=―― + ―― + ――
　　　∂x 　∂y　　∂z

を表している。これは特に「発散(divergence)」と呼ばれる。

二番目の式はナビエ・ストークス方程式の非圧縮性条件というもの。シミュレーションの単位となる各単位立方体に「入ってくる流体」と「出ていく流体」のトータルは「ゼロになる」という条件を与えて、一番目の式と連立させて方程式を解き、圧力pと速度uを求める。これは各単位立方体で質量保存則が維持され、流体が圧縮されないという条件設定に相当する。

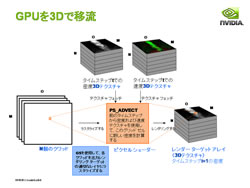
この仕組みをGPUで実装する際には前述したように速度、密度、圧力といったパラメータをテクスチャで持ち、GPUは、これらの3つのテクスチャから値を取り出してピクセルシェーダでナビエ・ストークス方程式を解き、求めた次の状態の速度、密度、圧力を新しいバッファ(テクスチャ)に書き出す。

なお、前述しているように、取り扱っているのは三次元空間での流体物理なので、テクスチャは配列構造とした3Dテクスチャとなっている。

シミュレーションの実際の計算を行う際にはDirectX 10/SM4.0の特徴であるジオメトリシェーダが活躍する。流体の計算自体は3Dテクスチャ上で行うわけだが、その3Dテクスチャが実際にシーンの3D空間上でどのように対応づけられるかを取り決めなければ行けないのだが、この仮想的なジオメトリ(仮想的なポリゴン)の生成をジオメトリシェーダに行わせるのだ。