今回からは 4 回の記事にわたって、アルゴリズムで解ける発展的な問題をいくつか紹介します。競技プログラミングの簡単な問題ではあまり出題されないアルゴリズムもありますが、本稿によって「アルゴリズムという武器を使えばこんな問題も解けるんだ」ということを体感していただけると嬉しいです。
二部マッチング問題
最初に紹介する問題は「二部マッチング問題」です。4 匹の犬 (A, B, C, D) と 4 匹の猫 (E, F, G, H) がいます。以下に示す犬と猫のペアは仲良しですが、それ以外のペアは残念ながら仲が良くありません。
- 犬 A と猫 E
- 犬 A と猫 F
- 犬 A と猫 G
- 犬 B と猫 G
- 犬 C と猫 H
- 犬 D と猫 G
仲良しの犬と猫のペアは、一緒に遊ばせることができます。それでは、最大で何組のペアを同時に遊ばせることができるのでしょうか。
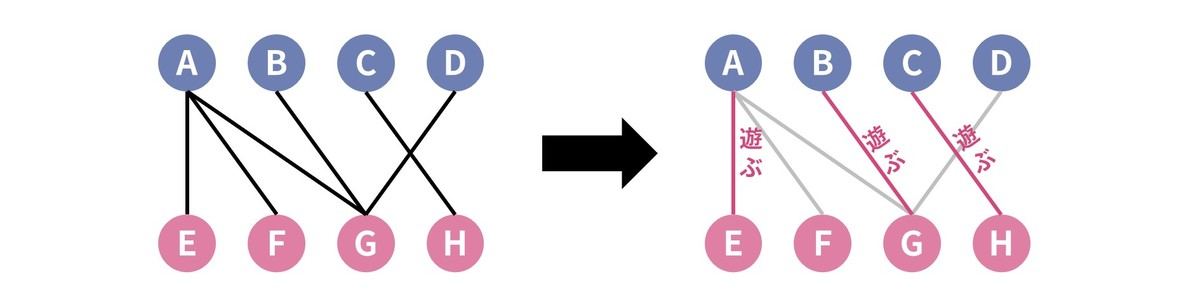
答えは 3 組です。例えば A と E、B と G、C と H を遊ばせると 3 組になりますが、ペアを 4 組つくることはできません。(イメージ図を以下に示します。この図では仲良しの犬と猫のペアを線で表しています)
このように、最大何組のペアを遊ばせられるかを求める問題を「二部マッチング問題」と言います。
直感的な解法と問題点
それでは、二部マッチング問題はどうやって解けば良いのでしょうか。一番直感的な解法は、「まだ選択可能な仲良しペアを適当に選び、遊ばせる」という操作を繰り返すことです。例えば、先ほどの例の場合は以下のようになります。
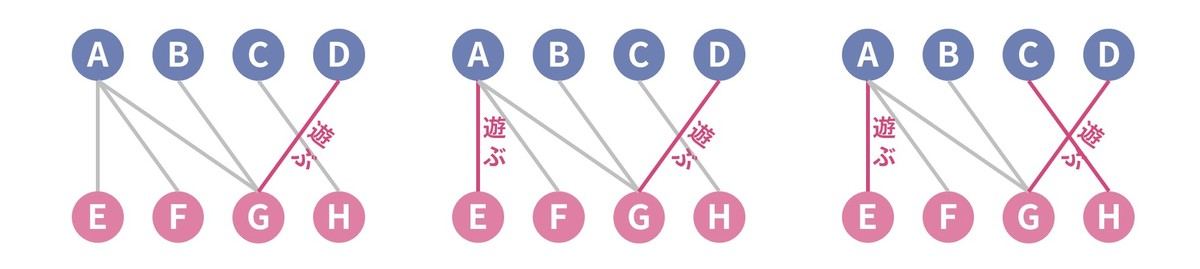
- まず、最初の時点ではどの仲良しペアも選択可能なので、適当に犬 D と猫 G を遊ばせます。(図の左から 1 番目)。
- 次に、現時点では (A, E), (A, F), (C, H) の 3 つの仲良しペアが選択可能なので※1、適当に犬 A と猫 E を遊ばせます。 (図の左から 2 番目)
- 最後に、現時点では仲良しペア (C, H) のみが選択可能なので、犬 C と猫 H を遊ばせます。 (図の左から 3 番目)
これで 3 組を同時に遊ばせることができました。
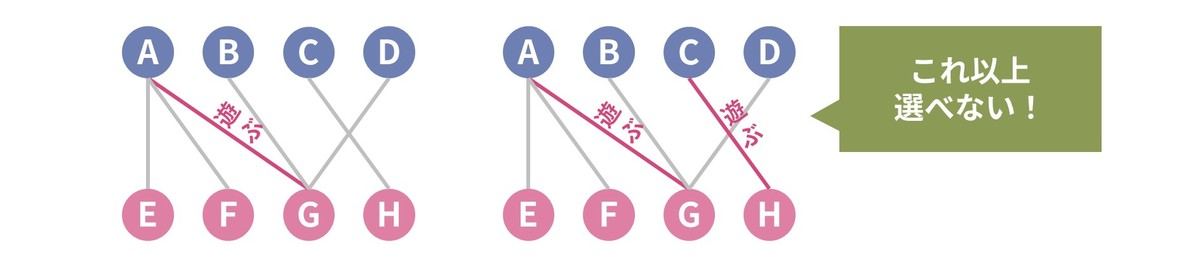
しかし、この方法は必ずしも上手くいくとは限りません。もし最初に犬 A と猫 G、犬 C と猫 H を遊ばせてしまった場合、これ以上仲良しペアを選ぶことができず、2 組しか遊ばせることができないのです。
※1:例えば、仲良しペア (B, G) は、猫 G がすでに遊んでしまっているので選択不可です。
正しい解法
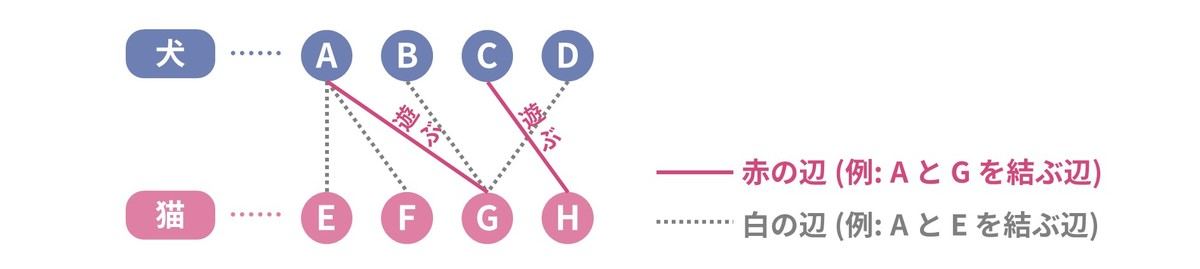
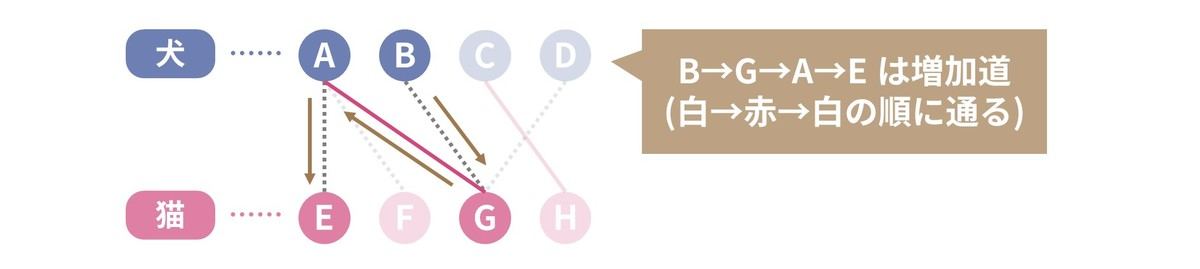
それでは一体どういう方法を使えば、必ず正しい答えを出すことができるのでしょうか。まず、すでに遊ばせたペアを「赤の辺」、まだ遊ばせていないペアを「白の辺」と呼ぶことにします。
また、犬側の頂点から出発した後、白の辺→赤の辺→白の辺→赤の辺→… を交互に通ってから、猫側の頂点に到着する経路のうち、同じ頂点を二度通らないものを増加道と呼びます。例えば、経路 B→G→A→E は増加道です。
このとき、「増加道を適当に選んで色を反転させる」をできなくなるまで操作を繰り返すと、必ず一番多くの組を遊ばせることができます※2。イメージが分からない方は下図をご覧ください。
なお、この増加道を反転させるアルゴリズムを使うと、もし犬と猫がそれぞれ 1000 匹ずついても、コンピューターを使えばたったの数秒で答えを出すことができます。
※2:証明は難しいので割愛させていただきます。
二部マッチング問題の応用例
ここまで紹介した二部マッチング問題は、実社会のさまざまな問題に応用することができます。今回は例として「会議スケジューリング問題」を紹介します。
あなたは 5 つの会議 A~E に参加しなければなりませんが、相手の都合上、各会議は以下の時間帯にしか設定できません。
- 会議A:13時台・14時台
- 会議B:14時台・15時台
- 会議C:14時台・16時台
- 会議D:13時台・17時台
- 会議E:14時台・16時台
また、同じ時間帯に複数の会議を設定することはできません。このとき、あなたは全ての会議に参加することができるのでしょうか。
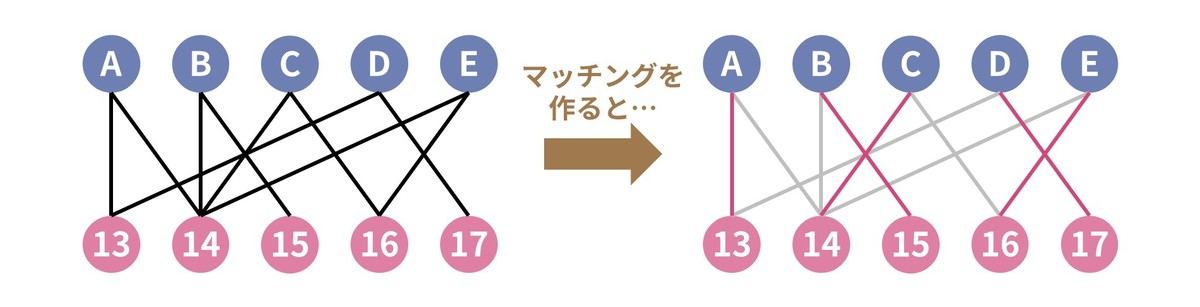
まず、“会議” と “時間帯” を頂点とし、“設定できる時間帯” を辺としたグラフを考えます。例えば、会議 A を 13 時台に設定することは可能なので、会議 A と 13 時台の間に辺を追加します。(グラフは下図のようになります)
すると、答えは二部マッチング問題そのものです。下図のように (A, 13), (B, 15), (C, 14), (D, 17), (E, 16) をマッチングさせると、5 組のマッチングができるので、5 個全部の会議に出席できることが分かります。
逆に、もしマッチングが最大 4 組しかなければ、4 つの会議にしか参加できない、つまり 1 つの会議を諦めなければならないと分かります。
このように、 “会議” と “時間帯” のマッチングを考えることで、会議スケジューリング問題を解くことができました。
その他の応用例
なお、二部マッチング問題に帰着して解ける問題は、会議以外にもたくさんあります。代表的な具体例としては、以下が挙げられます。
- 席替え (生徒と席のマッチング)
- シフト決め (労働者と時間帯のマッチング)
- 駅伝の走順 (選手と区のマッチング)