東京女子大学と新潟大学(新大)の両者は11月10日、計算機を用いた「精度保証付き数値計算法」、特に固有関数の誤差評価に関する最新理論を利用し、多角形領域における「ディリクレ境界条件」、「非斉次ノイマン境界条件」の形状微分に対する厳密計算法を確立したことを共同で発表した。

同成果は、東京女子大 数理科学科の劉雪峰教授、新大 自然科学研究科の遠藤凌輝大学院生の研究チームによるもの。詳細は、微分方程式の理論と応用に関する全般を扱う学術誌「Journal of Differential Equations」に掲載された。

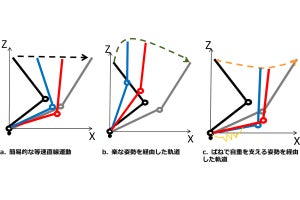
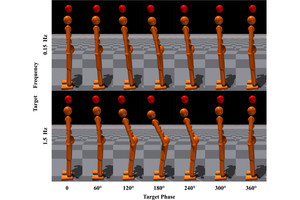
物体の振動する音から物体自身の形状を推定するという“逆問題”は、図形や多様体の形状を、そのラプラス作用素の固有値を用いて研究する数学の分野である「スペクトル幾何学」の基礎問題として知られる。太鼓の音(固有振動数)と太鼓の形状の関係は、数学的には“ラプラス作用素の固有値問題」￥”という偏微分方程式によって表現される。

なおラプラス作用素とは、微分方程式論において、非常に重要な役割を果たす2階微分作用素のことを指し、固有値問題とは、微分という演算に関してスケールが変わっても形状が保持される場合について、その数値(固有値)と対応する関数(固有関数)を求める問題のことをいう。

ラプラス作用素の固有値と領域の形状の関係を解析するためには、形状微分と呼ばれる「固有値問題の領域変数に関する微分値」の具体的な値を計算することが重要となる。研究チームによると、長らく形状微分に対する理論的な解析が行われてきたが、厳密な計算法の確立には至っていなかったという。

ラプラス作用素の固有値は、適当な領域の設定に対して正の無限大に発散する非負の実数列だ。固有値は、領域の形状、固有値の重複度、境界条件によって異なる振る舞いをするため、これらの問題を研究するにはそれぞれの場合に対して異なる方法が期待されるとのこと。その中でも、三角形の固有値に関する多くの問題は未解決のままだとする。

  • ラプラス作用素の固有値の分布

    ラプラス作用素の固有値の分布(出所:共同プレスリリースPDF)

そこで研究チームは今回、三角形領域に対する第1固有値の形状最適化問題に対し、ディリクレ境界条件(境界上での関数の値が0であるという条件)だけでなく、非斉次ノイマン境界条件(境界上における法線方向の微分が与えられているという条件)といった、複雑な境界条件を持つ問題にも対応可能な検証法の開発を試みたという。

そして、一定の直径を持つ三角形のうち、正三角形が最初のラプラス作用素の第1固有値を最小化することが、ディリクレと非斉次ノイマンの両境界条件のもと証明されたとした。

今回検討された非斉次ノイマン境界条件の固有値問題は、有限要素法による微分作用素の固有値の下界評価に由来している。なお有限要素法とは、方程式が定義された領域を小領域(要素)に分割し、各小領域における方程式を比較的シンプルな関数で近似する手法のことである。

劉教授は2015年当時、2次元領域におけるラプラス作用素の固有値λkに対し、公式という計算可能な下界評価式を導出。ここで、hは有限要素法による三角形メッシュのサイズであり、λk,hは「Crouzeix-Raviart有限要素空間」による離散化固有値であり、定数0.1893は「Crouzeix-Raviart補間誤差」の定数に密接しているとする。

またCrouzeix-Raviart補間誤差定数は、三角形領域における非斉次ノイマン境界条件を持つ固有値問題で特徴づけられる。今回の研究では、定数を決める固有値に対する三角形領域の形状最適化問題において、固有値の形状微分の範囲を厳密に算出する方法で、最大辺長が1の三角形の中で、θがπ/3の時の正三角形が、Crouzeix-Raviart補間誤差定数を最大化することを数学的に厳密に証明することに成功したという。また「0.1893」は、補間誤差定数の最大値としての良い近似値であり、最適な固有値の下界評価式を提供しているとした。

  • (左)三角形の形状変化。(右)補間誤差定数の値と角度θとの関係

    (左)三角形の形状変化。(右)補間誤差定数の値と角度θとの関係(出所:共同プレスリリースPDF)

今回の研究によって、近年開発された微分作用素の固有値と固有関数に対する精度保証理論を用いた評価により、形状微分の具体的な値を厳密に評価することが実現された。そして純粋に理論的な評価方法と比較して、固有値の形状最適化問題に対してより直接的な分析が可能になったとする。

また研究チームは今後の展開の方向として、「形状微分の精度保証付き数値計算」の拡張、そしてその応用という2つの方向を考えているという。潰れた領域やなめらかな境界を持つ領域において形状微分を厳密評価し、2階形状微分の具体的な値の厳密評価を可能にすることで、固有値に関する領域の形状最適化問題だけでなく、領域の形状決定問題「太鼓の形を聴く」の計算機援用証明に取り組んでいきたいと考えているとしている。