3Dモデルの変形までが可能な動的PRT(2)～SH LogとSH Expとは?

SH LogとSH Expとは?

SH LogのLogは対数を表している。そしてSH ExpのExpは指数を表す。

高校数学で習う公式に複数の掛け算(積)はその数のLogの総和(加算)をExpした値に等しいというものがある。

この指数と対数の法則をSH Triple Productに対して応用したのがSH LogとSH Expの計算になる。

つまり、遮蔽係数ベクトル同士のSH Triple Product演算負荷を低減するために、まず対数(Log)の和を計算し、その値に対して指数(Exp)を取ることでSH Triple Productを計算したことにならないか……というわけだ。これが成り立てば負荷の高いSH Triple Productの反復を単純な加算に落とし込めることになる。この証明はとても複雑なのでここでは省略するが、これは成り立つということで、使って良いことになっている。

SHEXP技法における事前計算の工夫

SHEXP技法での動的PRTでは、登場する3Dモデルを全て球体にしてしまう関係で、自己遮蔽やShadow Fieldsの事前計算を単一の球、1個に限定できる。ここで以降の演算を行いやすくするための工夫を施す。

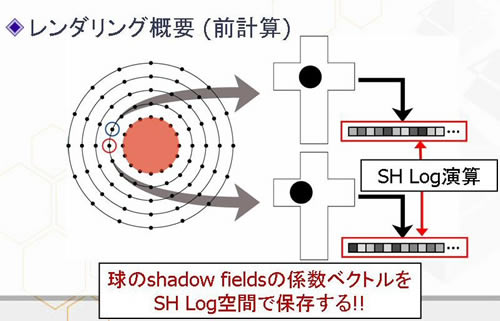
PSF技法では球面調和関数のスケーリング係数からなる遮蔽係数ベクトルを保持していたが、SHEXP技法では、SH LogとSH Expの仕組みを活用するために、この係数に対してあらかじめSH Log演算を行って、SH Log空間の値として持つようにする。

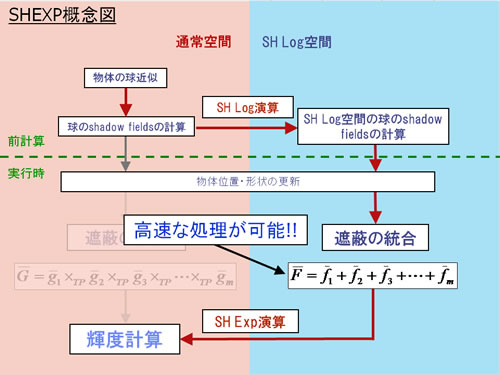
この工夫により、遮蔽構造の合成(統合)処理の中間計算を負荷の高いSH Triple Productではなく、加算のみで処理できるようになる。最後にSH Exp演算を行って元の空間に戻し、陰影処理(輝度計算)を行うようにする。

重い処理の一部をリアルタイムで行わず、事前に行っておくというイメージだ。これによりPSF技法ではとても高負荷だったSH RotationやSH Triple Productの演算の負荷が下がることにより、球が多数登場する球近似を用いるSH Exp技法においてもそこそこのパフォーマンスが見込めるようになる。(続く)

(トライゼット西川善司)