慶応義塾大学(慶大)は、温度を持ち多数の粒子からなる環境(熱環境)にさらされた系における確率分布を考察し、2つの分布間距離を熱力学第二法則によって定量的に記述される熱力学的不可逆性の度合いを使って解釈する関係式を見出したことを発表した。

同成果は、同大理工学部のヴー・バンタン研究員と齊藤圭司 教授によるもの。詳細は、米国物理学会誌「Physical Review X」(オンライン版)に掲載された。

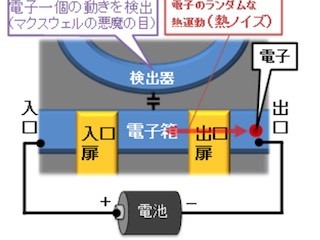
気体にはアボガドロ数とモル数を掛け合わせた分子の数が含まれ、その分子は互いに作用しあいながら、ニュートンの運動方程式に従って運動をしていることから、個々の分子の速度も決定できるとされるが、実際の気体の個数は膨大であり、個々の分子の運動を追うことは難しい。そこで、密閉された箱のような、ある領域に限った分子の速度分布を考えると、箱の内部の気体の温度が固定されていた場合、粒子の速度分布を表すマクスウェル分布で表すことが可能であり、これは領域が孤立した状態のみならず、同じ温度の熱環境に接していても変化することがない普遍的な分布であるとされている。

このような孤立した箱の体積をいきなり2倍にした場合であっても、内部の粒子はニュートンの運動方程式に従って運動するが、広がった気体は事実上、2度と元の体積内に収まることはなく、そうした元に戻らない熱力学的な性質は「熱力学的不可逆性」と呼ばれ、熱力学では熱力学第二法則(エントロピー増大の法則)として知られている。

近年の熱力学はナノスケールといった小さな系にも適用され、大きな熱的なゆらぎのある状況でも、さまざまな熱力学的性質が研究されるようになってきており、そうしたゆらぎの大きい熱力学は「ゆらぐ系の熱力学」として体系付けられ、活発に議論が交わされるようになっているという。

また、熱環境下にある熱力学的な物理的対象では「分布」が活躍し、不可逆性を示す熱力学的な時間の矢を理解する上での基盤になるとされているが、ある時刻である分布をとり、後の時刻で別の分布をとるとき、その分布の違い、あるいは分布の距離には、物理的にどのような意味が存在するのかについては、まだそれほど研究が進められていなかったという。

そこで研究グループでは今回、分布間の距離を特徴づけることを目的に、初期に配置された荷物を別の配置に配置換えするために必要な、動かす荷物の最小距離を定量化する数学的な量である「ワッサースタイン計量」に着目したとする。

ワッサースタイン計量は、もともと、初期に配置された荷物を別の配置に配置換えするために必要な、動かす荷物の最小距離を定量化する数学的な量です。全く別の荷物の配置を考え ると、移動する距離が遠いため、配置換えをするためには「苦労」をしなければなりません。その 苦労の度合いをワッサースタイン計量は数学的に定量化していると言えます。

熱力学における確率分布の文脈におけるワッサースタイン計量は、ある分布から別の分布に動かすために、確率分布の時間発展を与えるダイナミクスのもとでの分布の時間発展である確率過程のダイナミクスを考え、状態に割り当てられた分布を移動するためのコストを考える必要があり、そのコストが、熱力学的にどのような苦労が必要かを定量化してくれるものになると考えられ、研究グループでは、状態間レベルでのモビリティーという物理量を導入することにしたとする。

その結果、「熱力学的エントロピー」と「状態間のモビリティー」が確率分布間の距離と結びつき、ある分布から別の分布に移る際に、熱力学的な意味で支払わなければならないコストの度合いになることを見出したとする。

また、この関係を使うと、ある分布から別の分布への操作に要する時間に関して、熱力学的な限界を緻密に議論することが出来るようになるとしており、研究グループでは、この関係の応用として、情報処理で重要になる情報の初期化のスピードを定式化することにも成功したとしている。この成果は、計算と熱力学を時間の観点から結びつけるものであるとするほか、ダイナミクスが量子力学的な過程である場合でも、同様な定式化をすることに成功したともしている。

  • 分布から分布への変化の概念図

    分布から分布への変化の概念図 (出所:慶大プレスリリース)

なお、状態間のモビリティーという物理量は今回の研究で新しく導入されたものであるため、研究グループでは、今回の研究の文脈以外でどのように役立つかに関して、さらなる研究が必要になるとしている。また、今回得た確率分布変化に対する熱力学的解釈は、熱環境下で動作する計算機や量子デバイスの性能限界を理解するなどといった定量的応用などが期待されることから、より具体的な設定での研究が必要になるともしている。