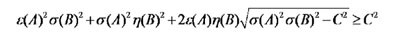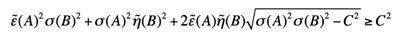東北大学は12月25日、量子力学の基本原理の1つである「測定誤差と擾乱に関する不確定性関係」に関して、「ハイゼンベルクの不等式」が破れており、「小澤の不等式」ならびに、2013年に新たに提案された「ブランシアードの不等式」が成立していることを、量子状態の弱値を得ることが可能な「弱測定」を用いた実験で検証することに成功したと発表した。

同成果は、同大電気通信研究所の枝松圭一 教授、名古屋大学大学院情報科学研究科の小澤正直教授らによるもの。詳細は2013年12月26日付の米国物理学会論文誌「Physical Review Letters」オンライン版に掲載される予定だ。

これまで研究グループは、量子力学の基本原理の1つである「測定誤差と擾乱に関する不確定性関係」として知られる「ハイゼンベルクの関係式」が破れており、名大の小澤教授が発見した新しい関係式(小澤の不等式)が成立していることなどを明らかにしてきたが、小澤の不等式のがε(A)=0またはη(B)=0ではない場合、両辺の等号が成立する場合があるのか、より厳しくかつ常に成立する不等式は存在するのかなどの疑問が残されていた。

こうした謎の解明に向け、2013年にはオーストラリア・クイーンズランド大学のCyril Branciard博士が小澤の不等式を改良し、ε(A)=0またはη(B)=0以外の場合にも等号が成立する場合がある、より厳しい関係式(ブランシアードの不等式)を導き出していた。

ブランシアードの不等式

また、同博士は、電子スピンの向きの測定や光子の偏光の測定の場合などにおいて成立するさらに厳しい不等式も導きだしており、この不等式が理想的な場合には両辺の間に等号が成り立つことが判明していたが、これらの不等式(ブランシアードの不等式)の実験的検証が求められていた。

電子スピンの向きの測定や光子の偏光の測定の場合などにおいて成立するブランシアードの不等式

そこで研究グループは今回、光の偏光に関する計測法「弱測定」を用いて、小澤の不等式とブランシアードの不等式が成立すること、ならびに測定された誤差と擾乱の関係が、ブランシアードの不等式が予言する限界に近いものとなっていることを実験的に確認することに成功した。

具体的には、光の量子である「光子」の偏光を用い、縦横方向の偏光測定の強度を変化させたときの、「縦横方向の偏光測定における誤差」および「その測定によって斜め45度方向の偏光が受ける擾乱」を計測。

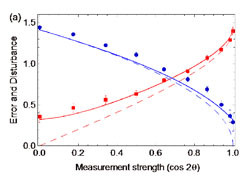
図2 MAにおける縦横方向の偏光測定の強度(横軸)を変化させたときの、「縦横方向の偏光測定における誤差(青線)」および「その測定によって斜め45度方向の偏光が受ける擾乱(赤線)」の計測結果。○と□が計測結果で、破線は理想的測定装置の理論値、実践は実際の測定装置の性能を加味した理論値。測定強度が大きくなるに伴い、誤差は減少する一方、擾乱は増大し、両者の間にトレードオフの関係があることがわかる

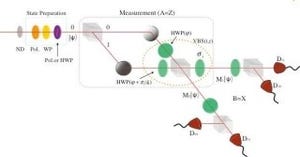
測定誤差と擾乱の計測に用いられた弱測定法は、誤差や擾乱の計測を行いたい実験装置(MA)の前段に弱測定の実験装置(WP)を配置し、WPの測定結果とMAの測定結果を比較することで、MAの誤差や擾乱を計測することができるもので、今回の実験では、測定の強さが弱いWPを採用し、測定対象となる系(=光子の偏光状態)をほとんど変えることなく、精密に誤差や擾乱を評価する手法を開発した(この測定系はブランシアードの不等式が成立するための必要な条件を満たしている)。

光子の偏光における弱測定法を用いた測定誤差と擾乱の計測装置。半導体レーザー(LD)から出た光は単一光子レベルまで減光された後、円偏光として装置に入射する。中央の黄色の部分が弱測定(WP)の実験装置で、縦横偏光(誤差の計測の場合)あるいは斜め45度方向(擾乱の計測の場合)のいずれかの偏光測定を弱い測定強度で行う。その後の水色の部分が主測定装置(MA)であり、縦横方向の偏光測定を種々の測定強度で行う。その後の紫色の部分(PM)は斜め45度方向の偏光測定を行う。各々の測定装置によって2光路のどちらかに出力された光子は、最後に8台の検出器のいずれかで検出される。光子がどの検出器で検出されたかによって、WP、MAおよびPMの測定結果がわかる。WPの測定結果とMA(PM)の偏光測定の結果を比較することで誤差(擾乱)を計測する

MAにおける測定の強度(横軸)を変化させたときの、誤差および擾乱に関する不等式の成立状況を見ると、図から、ハイゼンベルクの不等式の左辺は右辺を下回り、不等式が破れているのに対し、小澤の不等式ならびにブランシアードの不等式が保たれていることが分かった。特に、ハイゼンベルクの不等式の左辺は、不等式が予言する下限C=0.995に近い値となっており、同不等式において等号が成立する条件に近い状態が実現されていることが分かったほか、光学素子(偏光プリズム)の不完全性を考慮した場合の理論値と比べても実験値をよく再現していることが判明した。

MAにおける測定の強度(横軸)を変化させたときの、誤差および擾乱に関する不等式の成立状況。○や□などのマークは実験結果。破線は理想的測定装置の理論値で実線は実際の測定装置の性能を加味した理論値。青線がハイゼンベルクの不等式の左辺、赤のデータが小澤の不等式の左辺、紫および緑のデータがブランシアードの不等式の左辺。不等式の右辺はいずれもC=0.995で、中央のグレーの実線で表されている。ハイゼンベルクの不等式の左辺は右辺を下回り、不等式が破れているのに対し、その他の不等式は保たれていることが分かる。中でもブランシアードの不等式(緑側)の左辺の実験値は下限値C=0.995に近いことが分かる

さらに誤差と擾乱に関する測定結果と不等式の下限値を、誤差を横軸、擾乱を縦軸にプロットしてみると、実験び結果はハイゼンベルクの不等式を破り、他の不等式は満たす領域にあることが判明。このことは、2つの物理量(この場合は縦横方向偏光と斜め45度方向の偏光)に関する誤差と擾乱がハイゼンベルクの不等式から予言される下限値よりも小さいこと、つまり、2つの物理量がハイゼンベルクの不等式によって制限されると思われていたものよりも高い精度で同時に測定可能であることを示しているほか、実験結果は小澤の不等式を満たしているものの、小澤の不等式における下限値よりもかなり大きい領域にある一方で、ブランシアードの不等式の下限に近接しており、 理想的な実験を行った場合にはブランシアードの不等式が誤差と擾乱の関係の下限値を与えることが示された。

誤差と擾乱に関する測定結果と不等式の下限値を、誤差を横軸、擾乱を縦軸にプロットしたもの。黒丸は実験結果。黒点線は実際の測定装置の性能を加味した理論値。青の実線がハイゼンベルクの不等式、赤の点線が小澤の不等式、紫の破線および緑の一点鎖線がブランシアードの不等式における下限値。各々の下限値より左下方は不等式を破る領域で、実験値はハイゼンベルクの不等式を破り、他の不等式は満たす領域にある。特に、ブランシアードの不等式(緑線)の下限に近接していることがわかる

今回の研究について研究グループでは、新たに提案されたブランシアードの不等式に対する初の検証実験であり、小澤の不等式よりも厳しいブランシアードの不等式が検証されるとともに、誤差と擾乱が達し得る下限に関して新たな知見に達することができたとする。また、弱測定法は、誤差と擾乱を計測する以外にも、被測定系の状態を変化させずに物理量を計測する一般的な計測法として期待されてきており、今回の研究で用いた被測定系の状態をほとんど変化させないほぼ理想的な弱測定系の実現により、誤差と擾乱に関する明瞭な検証実験が可能になったで、物理のみならず科学技術一般に広く行われる「測定」という行為に対し根本的な制限を課す「不確定性関係」への見直しとなることはもちろん、従来の不確定性関係の枠を超えた超精密測定技術や新たな量子情報通信技術の開発などの多くの応用を拓くことが期待できるとコメントしている。

また、光子の偏光は、各々の測定結果は2通り(例えば縦偏光と横偏光のどちらか)となる点で、電子や中性子における「スピン」と同じ2次元系とみなせることから、今後は、さらに次元の高い物理状態や、ハイゼンベルクのガンマ線顕微鏡の思考実験で出てくる位置と運動量などのように、連続的な値を取り得る物理状態に対する不確定性を検証する実験にも取り組んでいき、不確定性に関するさらなる理解と応用を広げていければとしている。