東北大学と名古屋大学(名大)は7月17日、量子力学の基本原理の1つである「測定誤差と擾乱(じょうらん)に関する不確定性関係」として知られる「ハイゼンベルクの関係式」が破れており、名大の小澤正直教授が発見した新しい関係式が成立していることを、光を用いた実験で明瞭に検証することに成功したと共同で発表した。
成果は、東北大 電気通信研究所の枝松圭一教授、名大大学院 情報科学研究科の小澤教授らの研究チームによるもの。研究の詳細な内容は、英国時間7月17日付けで英オンライン総合学術誌「Scientific Reports」に掲載された。
ミクロな世界を支配する物理学の基本原理である量子力学では、2つの物理量(例えば位置と運動量)の測定に関して、一方の物理量の測定誤差と、その測定によって他方の物理量が乱される量(擾乱)との間には、一般に、一方を小さくしようとすれば他方を犠牲にしなければならないトレードオフの関係があるとされている。つまり、位置を知ろうとすれば運動量が不確かになり、運動量を知ろうとすれば位置が不確かになるというわけだ。
1927年、ハイゼンベルクは、有名な「ガンマ線顕微鏡の思考実験」において、物体の位置(x)を精密に測定しようとすると、測定に伴う反作用によって物体の運動量(p)が不可避的に乱されてしまうことを見出し、位置測定の誤差(ε(x))と運動量の擾乱(η(p))との間には画像1の関係式(1)が成立するものと考えた。その関係式を一般の物理量AとBに拡張したものが画像2の式(2)だ。これらの関係式(1)および(2)は、「ハイゼンベルクの測定誤差と擾乱に関する不確定性関係」または単に「ハイゼンベルクの不等式」と呼ばれている。

|

|
|
画像1(左):位置測定の誤差(ε(x))と運動量の擾乱(η(p))との間に成立する(1)。画像2:画像1の関係式を一般の物理量AとBに拡張した関係式(2)。どちらも「ハイゼンベルクの測定誤差と擾乱に関する不確定性関係」または「ハイゼンベルクの不等式」と呼ばれている |
|
ハイゼルベルクの不等式についての補足だが、まず量子力学での考え方から述べると、位置や運動量などの物理量は波動関数に作用する「演算子」として扱われる点がポイントだ。そして2つの演算子AとBを考えた時、AB=BAが成立する時、それらは「交換する」といい、[A,B]≡AB-BAを「交換子」と呼び、(2)式の右辺のAとBをくくる「〈 〉(山カッコ)」は、対象の物理状態に対する平均値を表す。
(2)式からAとBが交換する時、右辺は0となって、Aの誤差(ε(A))とBの擾乱(η(B))はどちらも0となり得ることがわかる。ところが、AとBが交換しない時には、右辺は一般的に0ではなく、Aの誤差(ε(A))とBの擾乱(η(B))との間に、一方が小さいと他方が大きくなる(特に、一方が0であれば他方は無限大となる)トレードオフの関係があることがわかるというわけだ。
さらに捕捉すると、ハイゼンベルクの不等式にはもう1つの不等式が存在する(画像3)。これを(*)式とする。右辺は(2)式と同じであるが、左辺のσ(A)、σ(B)は各々、対象の物理状態におけるAおよびBのゆらぎ(AとBをそれぞれ独立に観測した時に得られる結果のバラつきを標準偏差で表したもの)だ。

|
|
画像3。もう1つのハイゼルベルクの不等式。(2)式とは別物だが、一般的に同じ名称で呼ばれるため、混乱を招いている |
これらは、(2)式における測定誤差と擾乱とはまったく別の量であり、(2)と(*)とは物理的に異なる事柄を表している。それにも関わらず、どちらも同じく「ハイゼンベルクの不等式」(あるいは「ハイゼンベルクの不確定性関係」)と呼ばれているために、相当の混乱が生じているのが実は問題だった。
(*)式はロバートソンによって数学的に証明されていることから(従って常に成立する)、「ロバートソンの不等式」とも呼ばれる。(2)と(*)は物理的に異なる事柄を表しているとはいっても、厳密には、測定誤差と擾乱に関する不等式である(2)は、(*)にさらにある仮定を加えて導かれるので、もちろん無関係というわけではない。従って、(2)はそのような仮定の下でのみ成立するものであり、仮定が満たされない時には(今回の研究で検証したように)破れる場合があるのである。
量子力学の初等的教科書では大抵、(*)をハイゼンベルクの不確定性関係と呼んで(2)と区別していないため、大きな混乱を招いてしまっているのが現状だ。今回の研究でハイゼンベルクの不確定性関係の破れが検証されたのは(2)式についてであり、(*)式ではないことを念頭に置いていただきたい。
話を元に戻すと、従来、この(1)と(2)の式については一般的に成立するものと思われてきたが、前述したように小澤教授によってハイゼンベルクの不等式は無条件に成立するものではないこと、さらに運動量を乱さずに位置の測定が可能な特別な場合があることが理論的に見出され、2003年にハイゼンベルクの不等式に代わって常に成立する画像4の新たな関係式(3)が提唱された。この関係式(3)は、「ハイゼンベルク=小澤の測定誤差と擾乱に関する不確定性関係」または単に「小澤の不等式」と呼ばれている。
この小澤の不等式によって、測定誤差と擾乱の間のトレードオフの存在が初めて一般的に証明され、その正しい姿が明らかになった。これまでに保存法則による精密測定の限界や量子計算の精度限界の導出など応用され、また新しい量子通信技術への応用が研究されている。
このように小澤の不等式は、従来、信じられてきたハイゼンベルクの不等式(2)を置き換えるという非常に重要な発見であり、その実験的検証が待たれていた。昨年来、中性子や光を用いた実験によって、ハイゼンベルクの関係式(2)の破れと小澤の不等式(3)の実験的検証についての報告がなされ、科学界で大きな話題となっており、一般でも取り上げられた。しかし、それらは測定方法が限られていたことや、誤差や擾乱の計測精度が低いなどの問題があり、より一般的かつ明瞭な実験による検証が望まれていたのである。
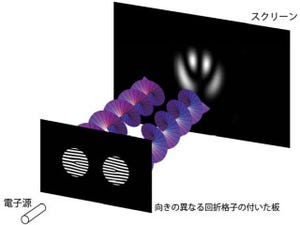
今回の研究では、光の量子である「光子」の「偏光」を用い、誤差と擾乱に関するハイゼンベルクと小澤の2つの不等式に対する実験的検証が行われた。なお偏光とは光の波(電磁波)としての振動方向のことをいい、1個の光子の偏光状態は、1つのスピンのように振る舞い、量子情報の基本単位である量子ビット(キュービット)としても利用される。光子の縦横方向における偏光測定の演算子と、斜め45度方向の偏光測定の演算子とは交換しないため、(2)あるいは(3)式の右辺が0ではなくなり、測定誤差と擾乱に関する不確定性関係の検証に利用できる仕組みだ。
枝松教授の研究チームはまず、光子の偏光を完全に正確に測定する「強い測定」から、何も測定しない「無測定」まで、その中間の「弱い測定」も含め、測定の強さ(精度)を連続的に変化させることができる実験系(画像5)を開発。また、測定誤差と擾乱の計測には小澤教授が発案した「3状態法」と呼ばれる方法が、光を用いた計測系として初めて採用された。
この実験系は、従来の報告例における実験に比べ、測定強度を変化させるというより一般的な測定を採用していることに加え、格段に明瞭な結果が得られることが特長だ。この技術を用いて初めて、測定誤差と擾乱に関するハイゼンベルクと小澤教授の両不等式についてのより一般的かつ明瞭な検証実験が可能になったのである。
画像5は、光子の偏光を用いた測定誤差と擾乱の計測装置の模式図。中央の枠で囲んだ部分が、縦横方向の偏光の測定部で、測定結果に応じて2つの異なる光路に光子が出力される。光学素子(HWP)の調節によって、測定強度を変化させることができる。2光路のどちらかに出力された光子は、次の測定部で斜め45度方向の偏光測定が行われる。ここで各々がさらに2光路に分かれ、最後に4台の検出器のいずれかで検出される。光子がどの検出器で検出されたかによって、縦横および斜め45度方向の測定結果がわかる。
画像6・7は、縦横方向の偏光測定の強度を変化させた時の、「縦横方向の偏光測定における誤差」および「その測定によって斜め45度方向の偏光が受ける擾乱」の計測結果を示したものだ。測定強度が大きくなるに伴い、誤差は減少する一方、擾乱は増大し、両者の間にトレードオフの関係があることがわかる。

|

|
|
縦横方向の偏光測定の強度(横軸)を変化させた時の、縦横方向の偏光測定における誤差(画像6(左))および斜め45度方向の偏光測定の擾乱(画像7)。丸印が計測結果で、測定強度が大きくなるに伴い、誤差は減少する一方、擾乱は増大する。破線は理想的測定装置の理論値、実線は実際の測定装置の性能を加味した理論値 |
|
そして、測定の強度を変化させた時の、誤差および擾乱に関するハイゼンベルクの不等式(2)の左辺、および小澤の不等式(3)の左辺を表したのが画像8だ。この実験では、不等式の右辺はどちらも1.0になる。図から明らかなように、ハイゼンベルクの不等式の左辺は右辺を下回り、不等式(2)が破れているのに対し、小澤の不等式(3)は保たれていることがわかるはずだ。
これらの結果により、光の偏光に関する測定強度を変化させるという、従来よりも一般的な測定(一般化測定、POVMなどと呼ばれる)においても、測定誤差と擾乱に関するハイゼンベルクの不等式(2)が破れ、小澤の不等式(3)が成立していくことが明らかとなったのである。
画像8は、測定の強度(横軸)を変化させた時の、誤差および擾乱に関する新旧の不等式の成立状況。丸印、破線および実線の意味は画像6・7と同じだ。下部のデータがハイゼンベルクの不等式(2)の左辺、上部のデータが小澤の不等式(3)の左辺。不等式の右辺はどちらも1.0であり、中央の実線で表されている。ハイゼンベルクの不等式の左辺は右辺を下回り、不等式(2)が破れているのに対し、小澤の不等式(3)は保たれているのがわかる。
量子力学が誕生してほぼ100年となるが、小澤の不等式の提案は、量子力学の根本にありかつよく知られた性質である不確定性関係に対して、100年来の常識を置き換えるという非常に重要なものだ。今回の研究成果は、光という身近な存在を用いて測定に伴う誤差と擾乱を精密かつ明瞭な形で計測し、ハイゼンベルクの不等式が破れる場合があること、そしてそのような場合でも常に小澤の不等式が成立することを明らかにした点が大きい。
また今回の成功は、物理のみならず科学技術一般に広く行われる「測定」という行為に対し根本的な制限を課す不確定性関係への見直しとなることはもちろん、従来の不確定性関係の枠を超えた超精密測定技術や新たな量子情報通信技術の開発など、多くの応用を拓くものであり、量子物理の基礎のみならず応用上も大変重要な成果だとする。
一方、小澤の不等式とその検証実験の意味するところに対しては大きな誤解も生じている。学会においても、小澤らの研究を契機として、不確定性関係の研究に関して新たな議論と展開が生まれようとしているという。量子力学や不確定性という問題は、一般にも大変興味深い話題であると同時に十分に理解するには難しい題材であるため、今回の研究や関連研究の結果とその意味するところについては、適切な広報活動によって一般にも正しく理解を広める努力が必要だと考えているとする。
今回の研究では、1個1個の光子の偏光の測定における誤差と擾乱を計測し、その関係がハイゼンベルクの不等式を破ることを検証し、小澤教授による新しい不等式を満たしていることが観測された。光子の偏光は、各々の測定結果は2通り(例えば縦偏光と横偏光のどちらか)となる点で、電子や中性子における「スピン」と同じ2次元系とみなされる状態だ。今後は、さらに次元の高い物理状態や、ハイゼンベルクのガンマ線顕微鏡の思考実験で出てくる位置と運動量などのように、連続的な値を取り得る物理状態に対する不確定性を検証する実験にも取り組みたいと考えているとした。そのような研究を通して、不確定性に関するさらなる理解と応用が広がるものと期待していると述べている。