日本学術振興会特別研究員の横山慶子博士および名古屋大学(名大)総合保健体育科学センターの山本裕二教授らの研究グループは、サッカーなどのパスで見られる3人のプレーヤ(3者)が互いの動きを見て、物理的にはつながれていないにも関わらず、あたかも何かでつながれているかのように、他の2者の動きを同時に感じて動く連携パターンを示し、それが対称性の破れにより説明できることを明らかにした。同成果は、「PLoS Computational Biology」に掲載された。
3という数はスポーツのみならず、日常生活で求められるチームワークでも基本とされており、これは2者よりも3者のほうがコミュニケーションの方法として様々なパターンが現れるためであると考えられている。
こうしたコミュニケーションのパターンは同期現象としてとらえることが可能だ。同期現象は、有機物、無機物問わず互いが意識せずに同期してしまう(例えば2つの振り子時計の振り子が同期する、蛍が同時に発光するなど)ことで、その原理解明に向けた研究も各所で進められている。その原理として考えられているものの1つに時空間的な対称性の破れから、新たな秩序が生じる「対称性ホップ分岐理論」がある。こうした現象はこれまでも動物の歩行パターンや粘菌の形成パターンなどで確認されたが、これらはいずれも物理的につながっているもので、3人以上の人が連携する場合にどのような同期現象が見られるのか、また対称性ホップ分岐理論で説明可能であるかどうかは不明であった。
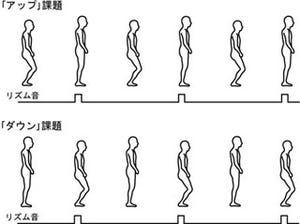
今回の研究では、サッカーの練習で行われる3対1練習での3者の動きを分析し、その連携パターンが対称性の破れから生じていると考えられることを明らかにした。具体的には、大学トップレベル、大学中級レベル、大学から初めてサッカーを始めたレベルの各選手に協力してもらい、3対1練習の風景をビデオで撮影、各選手の位置を記録し、その選手の位置から3名の選手でつくる三角形のそれぞれの角度を求め、その時間頻度を調査した。
その結果、上級者では○型、初級者では△型の分岐が確認され、これは環状に結合した3振動子に関して、対象性ホップ分岐理論で予測される回転パターンと部分逆位相パターンに相当するものであったという。
回転パターンは3つの角度が少しずつズレながら同期したパターンで、部分逆位相パターンは2つの角度が逆相同期で残り1つの角度は変化しないというもの。これを今回の3者の動きに当てはめると、上級者は常に残りの2者との関係をある一定に保とうと動くが、初級者は自分以外のどちらか1人のみとの関係で動いていることを示唆するものとなるという。

|
|
対称性ホップ分岐理論から予想される位相平面上の軌道。A、C、Fは上から順に回転パターン、部分逆位相パターン、部分同位相パターンにおける3者の角度の時間変化を示す。B、D、Gはこれらの角度変化を位相平面上で表したもので、E、Hは部分逆位相パターンと部分同位相パターンで一定となる角度が60度よりも大きい場合と小さい場合を表している |
この結果は、これまでの対称性ホップ分岐理論での説明例と同様に、物理的なつながりのない人の運動においても、何かにつながれているかのように同期していることを示しており、かつ回転パターンよりも部分逆位相パターンの方が対称性の破れの程度が大きく、上級者の方が初級者よりも対称性を保持していることを示すものとなった。
つまり、上手な選手は常に自分以外の2者の動きに気付いているため対称性を保つことが可能だが、上手くない選手は1人の他者の動きにしか気付かないため、対称性が破れてしまうということが考えられるとのことで、これは2者間の対人関係であれば、接近と回避を一次元的に振舞うことで説明できるが、3者間では2者との接近と回避運動が要求され、結果的に2次元における立ち位置の転回が必要になることが示唆されると研究グループでは説明しており、これは日常生活の中での3者以上の対人関係のあり方に示唆を与えるものであるほか、サッカーなどのチームスポーツでの連携を高めるための練習方法の考案などにもつながるものとしている。